11.15. Truncated dodecadodecahedron
|
[zurück] | 11.15. Truncated dodecadodecahedron |
[vor] | |
 |
 |
| Isometrie | Dimetrie |
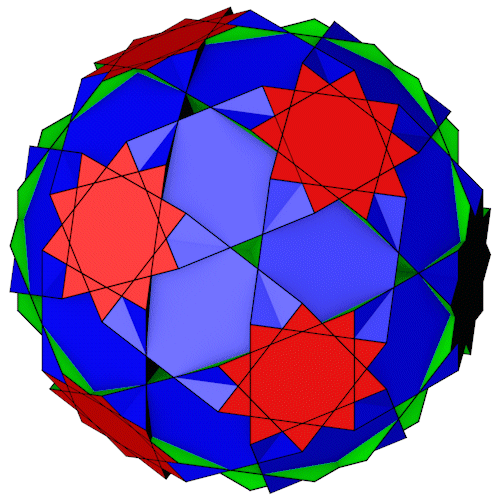
| Name | Truncated dodecadodecahedron Quasitruncated dodecadodecahedron |
| Anzahl Ecken | 120 |
| Anzahl Kanten | 180 |
| Anzahl Flächen | 30 Vierecke 12 Zehnecke 12 Dekagramme |
| Kantenlänge | 1 |
| Umkugelradius |  |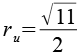
| Kantenkugelradius |  |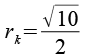
| Inkugelradius (Vierecke) |  |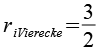
| Inkugelradius (Zehnecke) |  |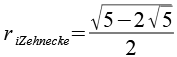
| Inkugelradius (Dekagramme) |  |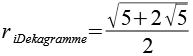
nur Vierecke
nur Zehnecke
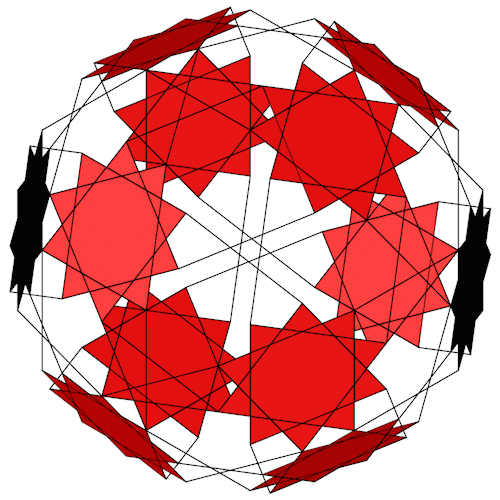
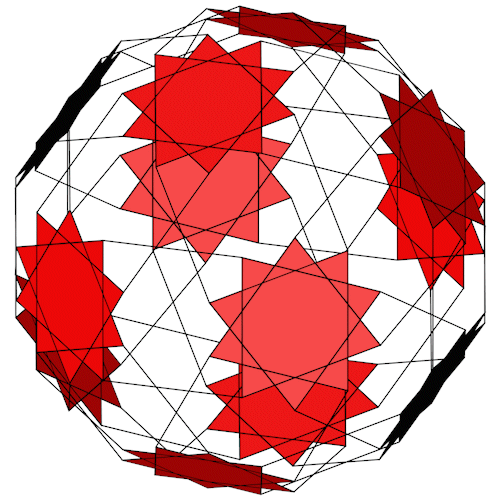
nur Dekagramme
Der Truncated dodecadodecahedron mit seiner Umkugel.
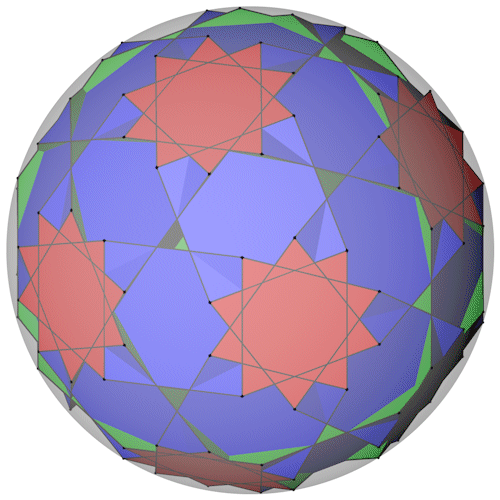
Der Truncated dodecadodecahedron mit seiner Kantenkugel.
Der Truncated dodecadodecahedron mit seiner Inkugel (Vierecke). Die Inkugel (violett) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt.
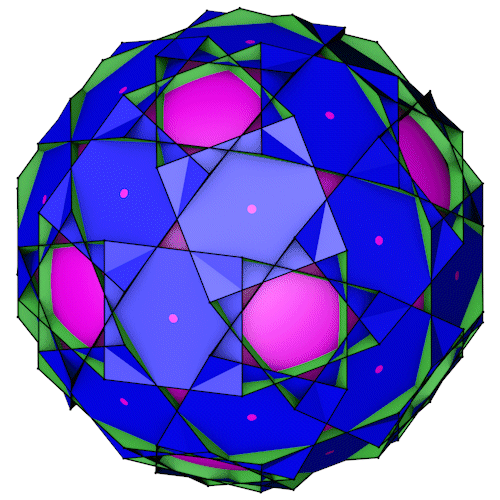
Der Truncated dodecadodecahedron mit seiner Inkugel (Zehnecke). Die Inkugel (violett) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt.
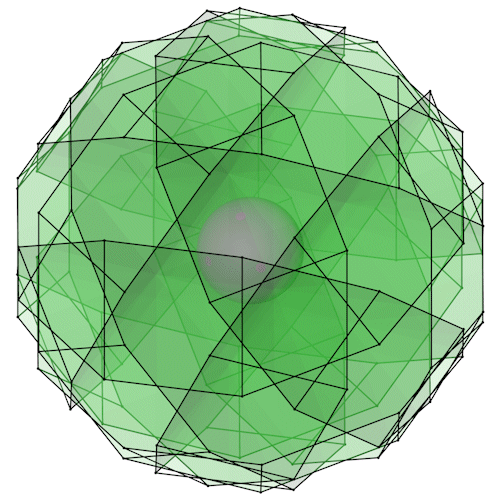
Der Truncated dodecadodecahedron mit seiner Inkugel (Dekagramme). Die Inkugel (violett) ist zur Veranschaulichung so dimensioniert das sie gerade so die entsprechende Fläche durchdringt.
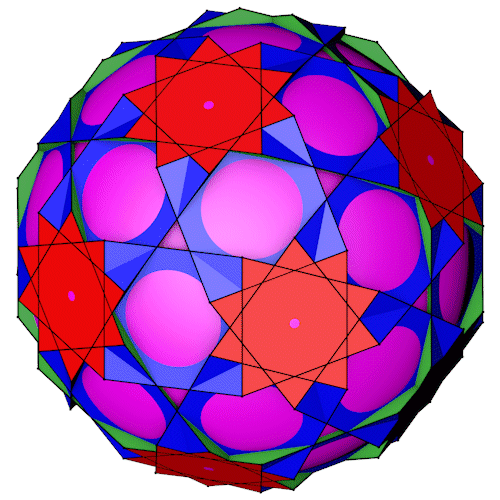
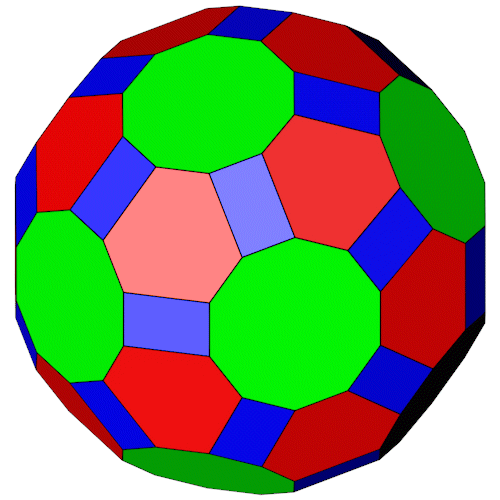
Die konvexe Hülle des Truncated dodecadodecahedron ist ein "Near Miss" Großes Rhombenikosidodekaeder . Nur die Zehnecke sind regulär.
 |
 |
| Konvexe Hülle des Truncated dodecadodecahedron | Großes Rhombenikosidodekaeder |
Der Truncated dodecadodecahedron mit seiner konvexe Hülle.
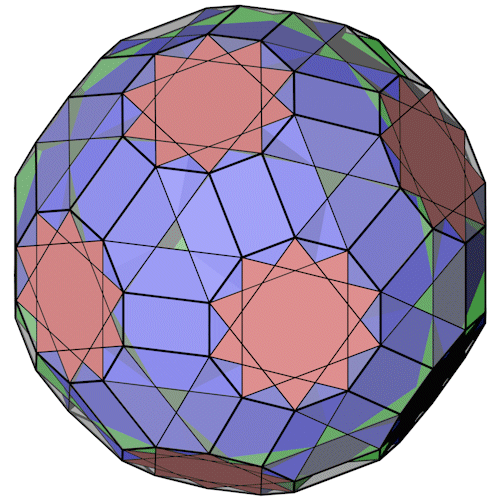
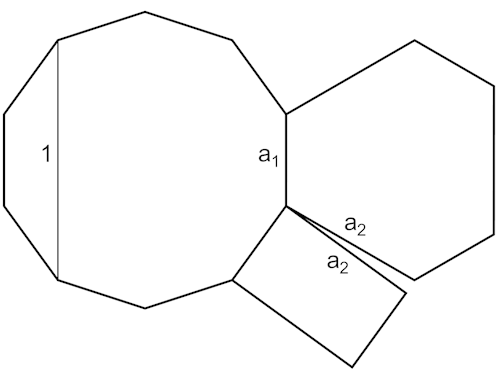
Die Polygone der konvexen Hülle, die Diagonale d3 des Zehnecks entspricht der Kantenlänge 1 des Truncated dodecadodecahedron. Phi ist der goldene Schnitt.
|
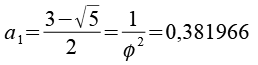
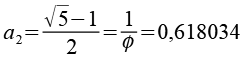
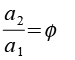
[zurück] | [Inhaltsverzeichnis] | [vor] | |