11.2. Pentagonaler Ikositetraeder
|
[zurück] | 11.2. Pentagonaler Ikositetraeder |
[vor] | |
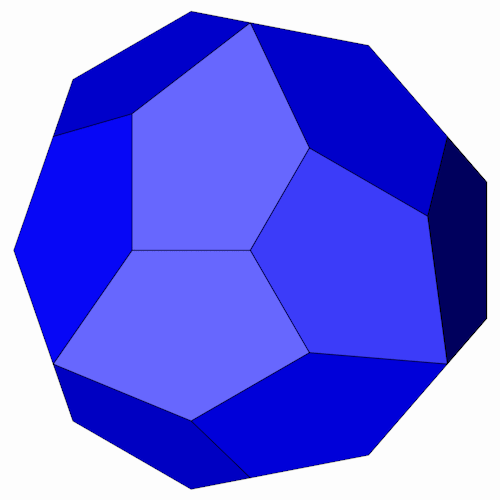
Wie beim Rhombic Propello Octahedron werden die Eckpunkte des Pentagonaler Ikositetraeder nur aus ganzen Zahlen gebildet, hier 0, 3, 9, 10, 15 und 20 [9].
 |
 |
| Isometrie | Dimetrie |
| Name | Pentagonaler Ikositetraeder |
| Anzahl Ecken | 38 |
| Anzahl Flächen | 24 unregelmäßige Fünfecke |
Die Seitenansichten.
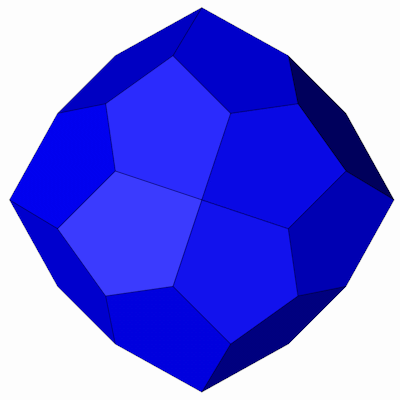
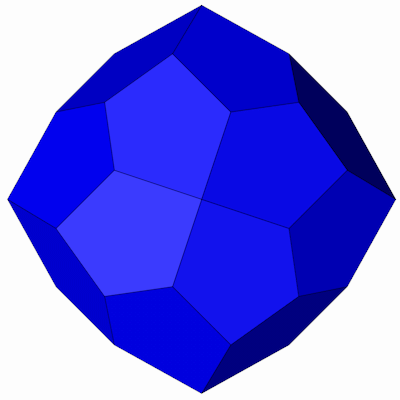
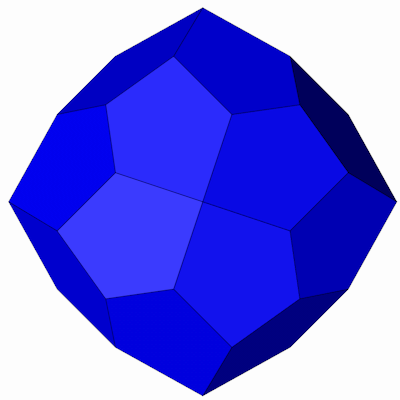
Der Pentagonale Ikositetraeder mit seiner Inkugel.
Der Pentagonale Ikositetraeder besitzt keine echte Kantenkugel aber eine Kugel die zumindest 3 Seiten der Fünfecke berührt.
Die Koordinaten der Eckpunkte des Pentagonalen Ikositetraeders lassen sich aus folgenden Beziehungen herleiten.
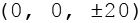
Daraus werden die 3 geraden Permutationen gebildet, andere gibt es in diesem Fall auch nicht.
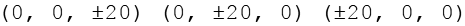
Durch Variation der Vorzeichen ergeben sich die ersten 6 Punkte. Für die nächsten Punkte gilt.
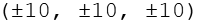
Durch Variation der Vorzeichen ergeben sich die nächsten 8 Punkte. Für die restlichen Punkte gilt.
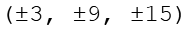
Daraus werden alle Permutationen gebildet, die 3 geraden Permutationen (links) und die 3 ungeraden Permutationen (rechts).
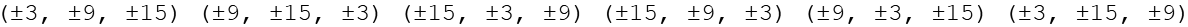
Durch Variation der Vorzeichen ergeben sich insgesamt 48 Punkte.
Aus den 48 Punkten werden 24 ausgewählt (rot). Von den geraden Permutationen alle mit ungerader Anzahl Minuszeichen und von den ungeraden Permutationen alle mit gerader Anzahl Minuszeichen.
Werfen wir noch einen Blick auf das unregelmäßige Fünfeck.
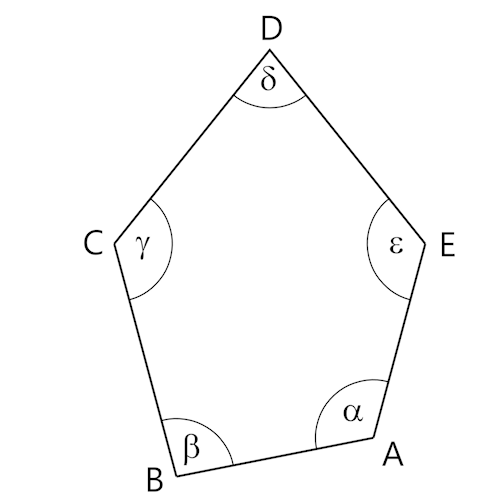
Für die Kantenlängen gilt.
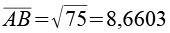
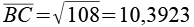
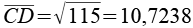
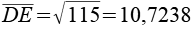
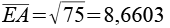
AB = EA und CD = DE. Die "Spitze" des Fünfecks ist ein gleichschenkliges Dreieck.
Für die Diagonalen gilt.
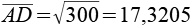
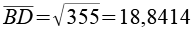
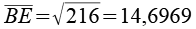
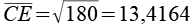
Über den Cosinussatz der Dreiecke lassen sich die Winkel berechnen.
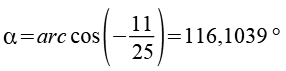
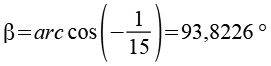
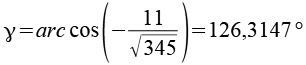
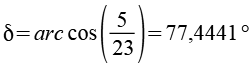
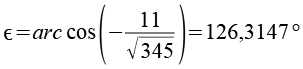
Die Summe aller Winkel beträgt 540°.
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |