4.1. Triakistetraeder
|
[zurück] | 4.1. Triakistetraeder |
[vor] | |
 |
 |
| Isometrie | Dimetrie |
| Name | Triakistetraeder Triakis tetrahedron |
| Anzahl Ecken | 8 |
| Anzahl Kanten | 18 |
| Anzahl Flächen | 12 gleichschenklige Dreiecke |
| Kantenlänge | a |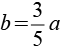
| Innenkugelradius |  |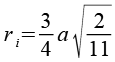
| Kantenkugelradius |  |
Die Seitenansichten.
Der Triakistetraeder läßt sich in einen Hexaeder einpassen.
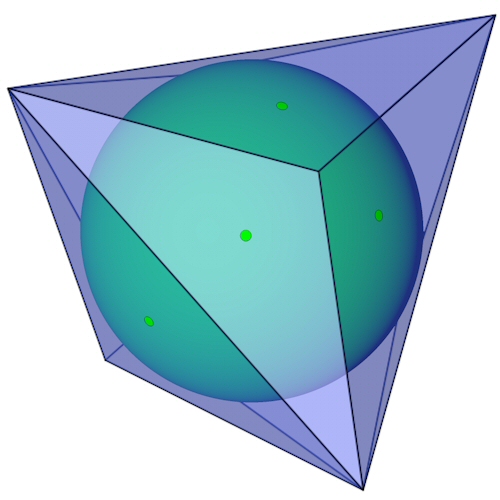
Der Triakistetraeder mit seiner Innenkugel.
Der Triakistetraeder mit seiner Kantenkugel.
Die Koordinaten der Eckpunkte des Triakistetraeders lassen sich aus folgenden Beziehungen herleiten.
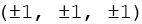
mit
Durch Variation der Vorzeichen werden jeweils 8 Punkte gebildet.
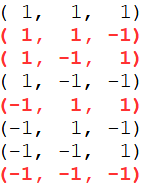
Aus den oberen 8 werden die Punkte ausgewählt, die eine gerade Anzahl Minuszeichen haben. Aus den unteren 8 werden die Punkte ausgewählt, die eine ungerade Anzahl Minuszeichen haben. Die anderen Punkte bilden einen komplementären Triakistetraeder.
Für die Kantenlängen a und b gilt.
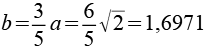
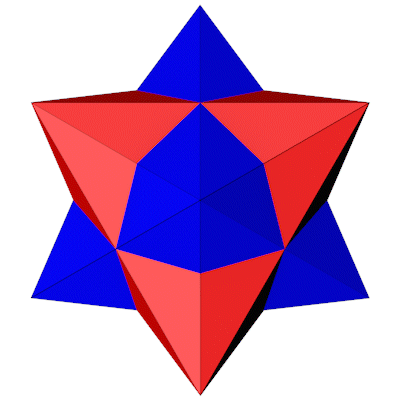
In der nächetn Abbildung sind die beiden komplmentären Formen blau und rot gefärbt.
 |
 |
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |