| [zurück] | 9.19. Oktaederstumpf mit 6-Eck Prismen und Quadratkuppeln |
[vor] |
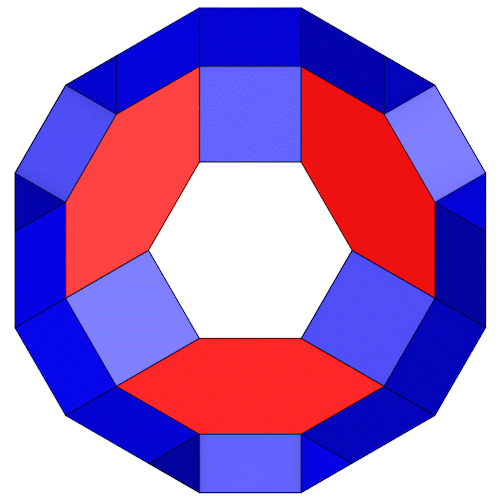
Diesen interessanten Polyeder mit Tunneln habe ich von [9] bekommen. Alle Polygone haben die gleiche Kantenlänge (1), nur die Sechsecke sind nicht regulär.
 |
 |
| Isometrie | Dimetrie |
| Anzahl Ecken | 96 |
| Anzahl Flächen | 84 Vierecke 12 Sechsecke |
Die Seitenansichten.



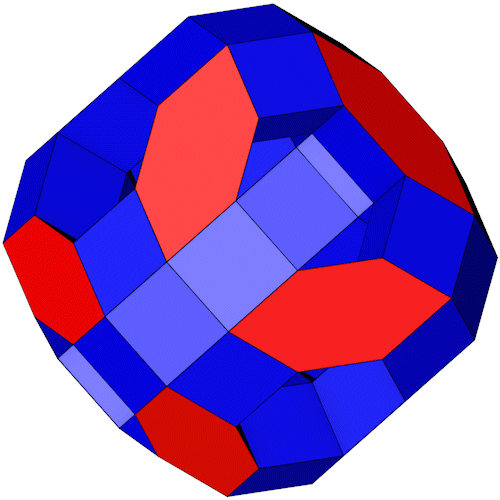
Der Polyeder aus einer anderen Perspektive.
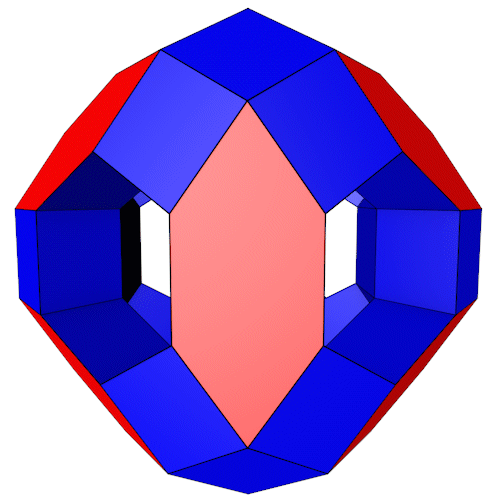
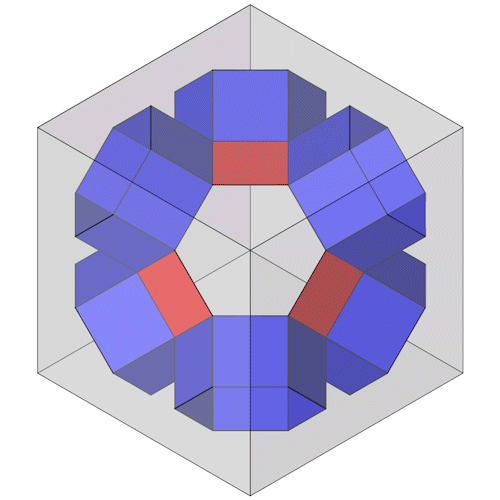
Um den Aufbau des Polyeders zu verstehen fangen wir im Zentrum an. Basis ist ein Oktaederstumpf, auf dessen Sechsecke 6-Eck Prismen gesetzt werden. Vom Oktaederstumpf bleiben nur 6 Vierecke (rot) erhalten.
 |
 |
Diese Struktur ist sehr symmentrisch wie man in der Draufsicht sehen kann.

Sie läßt sich von einem Würfel mit der Kantenlänge aWürfel umschreiben, jeweils 4 Kanten der 6-Eck Prismen berühren eine Seite des Würfels.
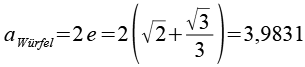
 |
 |
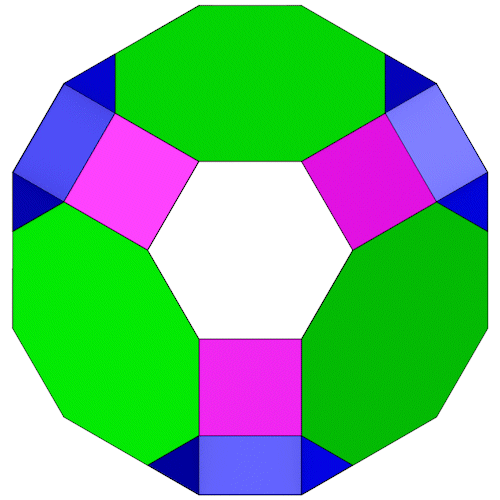
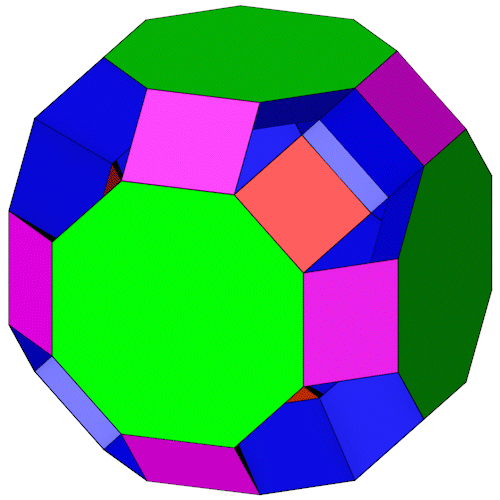
Zwischen den 6-Eck Prismen lassen sich Achtecke (grün) einfügen, die Lücken schließen wir mit Vierecken (violett). Man erhält dadurch im Prinzip ein "Near Miss" Großes Rhombenkuboktaeder, die Achtecke und die Vierecke sind aber nicht regulär.
 |
 |
Vergleichen wir dieses Konstrukt mit dem richtigen Großen Rhombenkuboktaeder bei gleichem Maßstab.
 |
 |
| Großes Rhombenkuboktaeder |
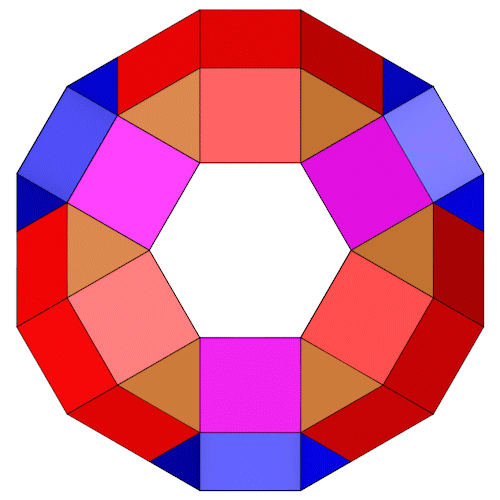
Die Achtecke ersetzen wir durch passende Viereckkuppeln (rote Vierecke und braune Dreiecke). Die Vierecke sind regulär, die Dreiecke sind gleichschenklig.
 |
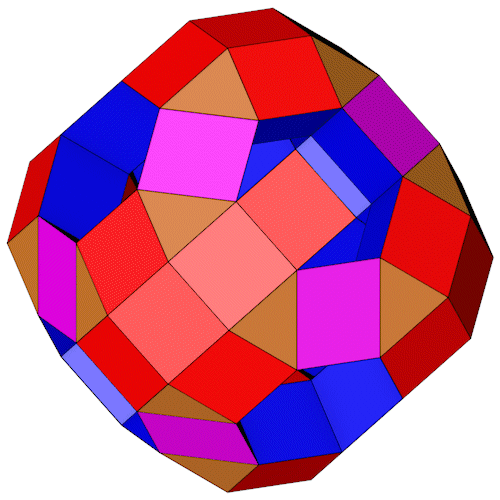 |
Im Prinzip ist der Polyeder jetzt fertig, wir können aber noch jeweils ein Viereck (violett) und zwei Dreiecke (braun) zu einem Sechseck zusammenfassen. Auch wenn das Sechseck nicht regulär ist haben jetzt alle Polygone die gleiche Kantenlänge.
 |
 |
Die Koordinaten der Eckpunkte des Polyeders lassen sich aus folgenden Beziehungen herleiten.
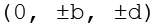


mit
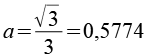
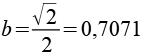
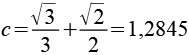

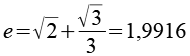

Aus
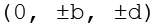
werden alle 6 Permutationen gebildet.
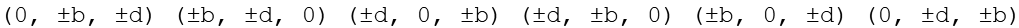
Durch Variation der Vorzeichen ergeben sich die ersten 24 Punkte. Aus

werden alle 6 Permutationen gebildet.
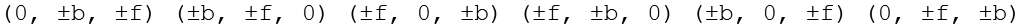
Durch Variation der Vorzeichen ergeben sich die nächsten 24 Punkte. Aus

werden alle 6 Permutationen gebildet.

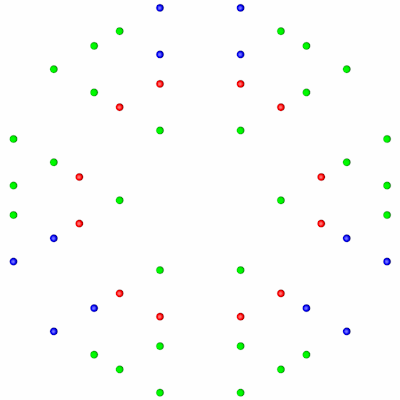
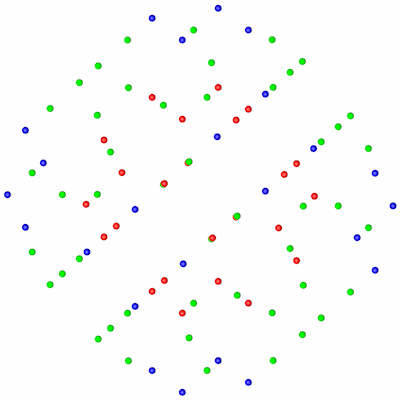
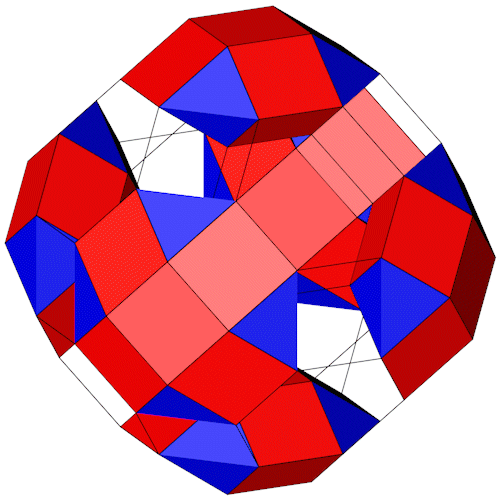
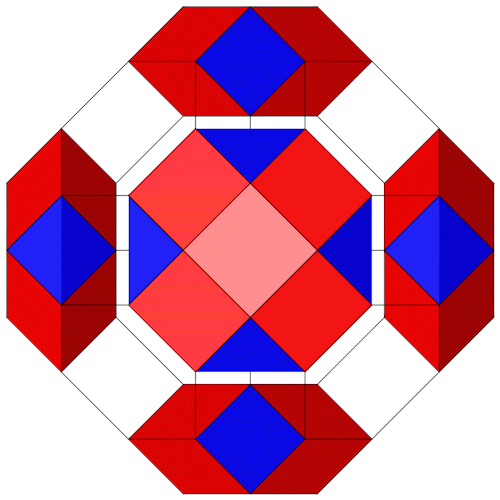
Durch Variation der Vorzeichen ergeben sich die restlichen 48 Punkte. Untersuchen wir welche der drei Beziehungen welche Punkte erzeugen, dazu habe ich sie rot, blau und grün gefärbt.
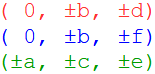
 |
 |
 |
| Isometrie | Dimetrie | Draufsicht |
Werfen wir nun einen Blick auf das Achteck.
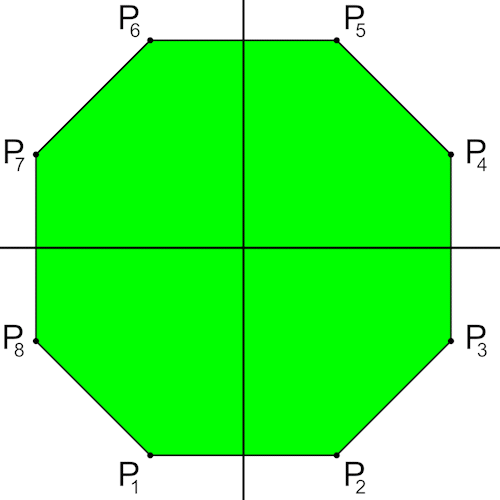
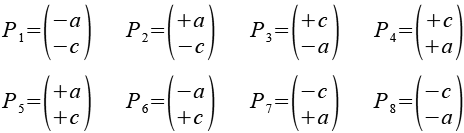
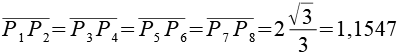
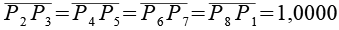
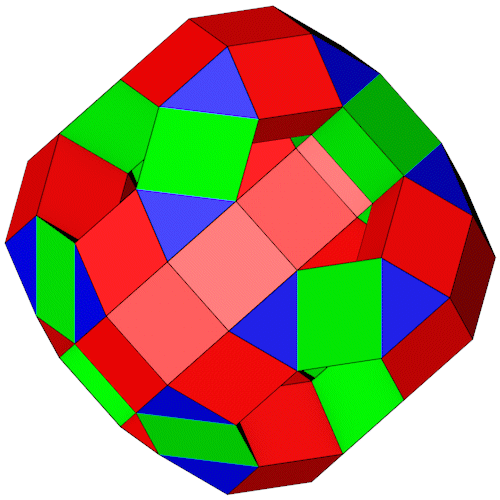
Dieser Polyeder läßt sich auch anders herleiten. 6 passende "Near Miss" Quadratdoppelkuppeln (Johnson Körper J28) werden so positioniert dass sie mit 6 "Near Miss" 3-Eck Prismen (grün) verbunden werden können.
 |
 |
 |
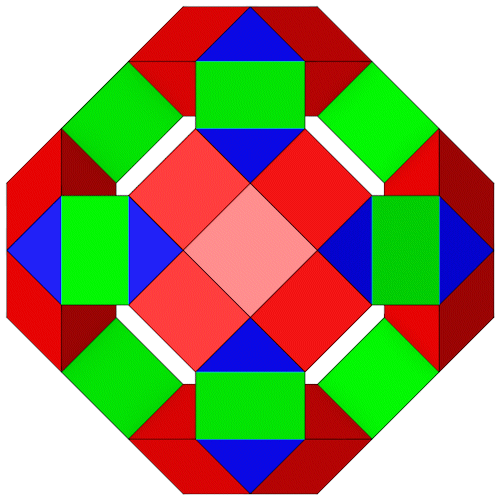 |
| Dimetrie | Draufsicht |
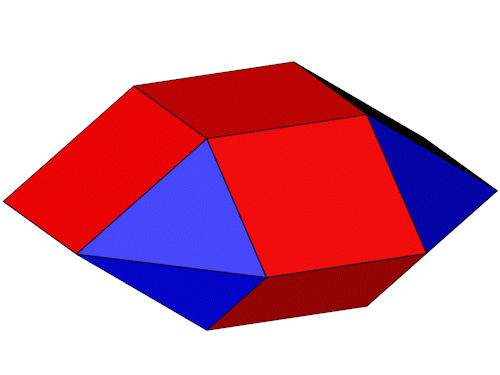
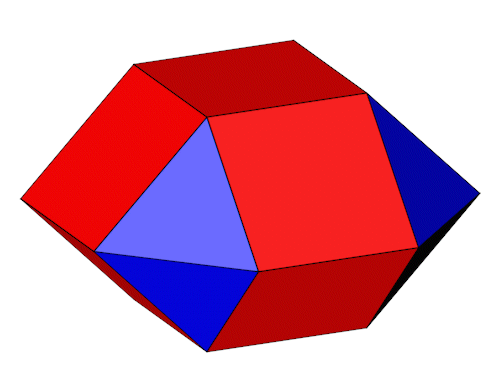
Vergleichen wir die "Near Miss" Quadratdoppelkuppel mit der Quadratdoppelkuppel (gleicher Maßstab).
 |
 |
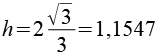 |
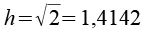 |
| "Near Miss" Quadratdoppelkuppel | Quadratdoppelkuppel J28 |
| [zurück] | [Inhaltsverzeichnis] | [vor] |