| [zurück] | 3.1. Gyroid Surface |
[vor] |
Die Gyroid Surface habe ich hier [1, 3, 5, 24, 44, 53, 55, 60, 61, 62, 63, 64] gefunden, sie wird durch folgende Gleichung dargestellt.
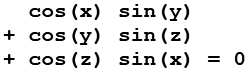
In den Gyroid lassen sich 18 Zylinder mit dem Radius pi/4 einpassen.
Die Löcher sind nicht ganz kreisrund, ein Loch in der x,z Ebene habe ich mal in höherer Auflösung berechnet. Der Mittelpunkt des Loches liegt bei x = pi/2 und y = 0. Das Bild zeigt einen Ausschnitt x = 0,77 bis x = 2,37, y = -3,5 bis y 3,0 und z = -0,8 bis z = 0,8. Für dieses Bild wurden 16.640.000.000 Punkte berechnet. Der schwarze Kreis zum Vergleich hat eine Radius von pi/4.
Wenn man die Schnittmenge des Gyroids mit einer Kugel berechnet erhält man ein besonders schönes Bild.
Eine Kugel mit dem Radius 2 pi, jeweils in der Ansicht Isometrie, Dimetrie und Oben.
Eine Kugel mit dem Radius 4 pi, jeweils in der Ansicht Isometrie, Dimetrie und Oben.
Die Gyroid Surface läßt sich auch durch eine alternative Gleichung [?] dargestellen.
Das beide Gleichungen identisch sind habe ich hier bewiesen (Gyroid-Formel.pdf).
Zum Schluß noch ein Bild des Gyroids in hoher Auflösung. Berechnet wurden 1 Milliarde Punkte, das Polygonobjekt besteht aus ca. 20 Millionen Punkten. Die Rederzeit betrug 1 h 45 min.
Wenn man den Sinus durch Cosinus ersetzt erhält man ebenfalls ein interessantes Objekt.
![]()
| [zurück] | [Inhaltsverzeichnis] | [vor] |