| [zurück] | 2. Python Scripts |
[vor] |
Für die Enwicklung des Scripts habe ich die Schwarz P Surface ausgesucht, sie wird durch folgende Gleichung dargestellt.
Für die Berechnung werden in einem Würfel mit der Kantenlänge 2 pi alle Raumpunkte einmal abgefragt ob sie der oben genannten Gleichung genügen. Wenn das Ergebnis der Berechnung kleiner als der Parameter delta ist dann gehört dieser Raumpunkt zur Schwarz P Surface. An dieser Stelle wird dann ein kleiner Würfel erzeugt.
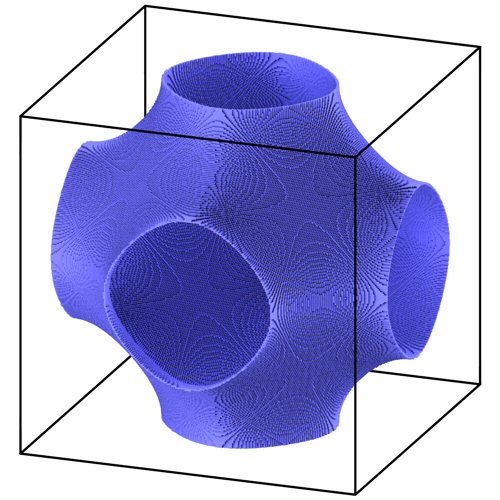
Delta muss so gewählt werden dass gerade eine geschlossene Oberfläche entsteht (Unterteilung Kante = 250). Ist der Wert zu klein entstehen Lücken in der Oberfläche, ist der Wert zu groß ist die Wandstärke zu dick.



delta = 0,012
delta = 0,020
delta = 0,05
Der Nachteil dieses Scripts (Test-1.py) ist die unbekannte Größe des Polygonobjektes, da zu Beginn der Berechnung nicht bekannt ist wieviel Punkte zur Figur gehören. Ich habe dann die Berechnung der Punkte von der Erzeugung des Polygonobjekts getrennt (Test-2.py). Die Punkte werden zuerst in einer Liste zwischengespeichert und auf dessen Basis wird dann das Polygonobjekt erzeugt. Es empfiehlt sich trotzdem hinterher beim Polygonobjekt das Mesh zu optimieren.
Je feiner der Würfel bzw. eine Kante unterteilt wird, desto präzieser wird die Figur.



Unterteilung 50
Unterteilung 100
Unterteilung 250



Unterteilung 500
Unterteilung 750
Unterteilung 1000
Mit zunehmender Unterteilung steigt der Rechenaufwand exponentiell an, bei einer Kantenunterteilung von 1000 müssen immerhin 10003 bzw. 1 Milliarde Punkte berechnet werden. Mein älterer Rechner benütigte für die Ausführung des Scripts ca. 9 min, das Rendern des Bildes dauerte ca. 11 min.
Einige Figuren kommen besser zur Geltung wenn man sie radial (Radius 4 pi) beschneidet (Test-3.py), hier am Beispiel des Gyroids. Berechnet wurden 1 Milliarde Punkte, das Polygonobjekt besteht aus ca. 20 Millionen Punkten. Die Rederzeit betrug 1 h 45 min.
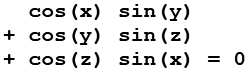
Ich habe de Würfel zusätzlich in 8 Teile geteilt die nacheinander berechnet werden müssen, so kommt man schneller zu einem Teilergebnis und eine höhere Auflösung ist möglich (Test-4.py, Testt-5.py), hier am Beispiel der Gleichung 10.4.2. Berechnet wurden insgesamt 4,096 Milliarden Punkte, das Polygonobjekt besteht aus ca. 20 Millionen Punkten. Die Rederzeit betrug 3 h 40 min.
![]()
| [zurück] | [Inhaltsverzeichnis] | [vor] |