[zurück]

2.101 Coupled Logistic Map

[vor]

Die Coupled Logistic Map habe ich hier [110, 233, 234, 235, 236, 237, 238, 239, 240] gefunden.

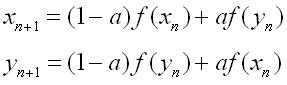
Die Funktion f(x) ist wie folgt definiert.

Die Gleichungen lassen sich durch Einsetzten verbinden.

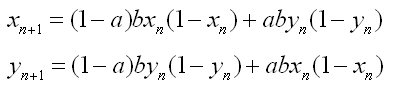
Pluginmenü

a = 0,012 und b = 3,7

Neuberechnung mit 100 Millionen Punkten

a = 0,014 und b = 3,7

a = 0,02 und b = 3,7    Berechnung mit 100 Millionen Punkten

a = 0,04 und b = 3,7

a = 0,057 und b = 3,7

a = 0,0574 und b = 3,7

a = 0,0604 und b = 3,7

a = 0,0674 und b = 3,7

Bei a = 0 und b = 3,5 besteht die Struktur nur aus 4 Punkten. Je nach Startwert haben die Punkte eine andere Symmetrie, davon gibt es 4 Varianten.

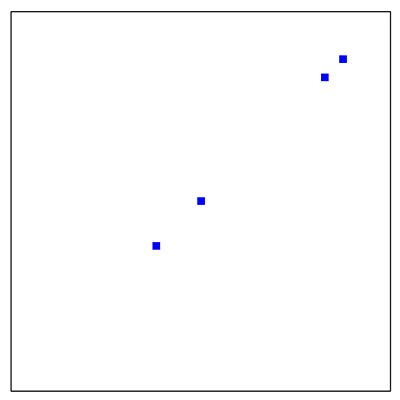
x_o = 0,1 und y₀ = 0,1

x_o = 0,3 und y₀ = 0,1

x_o = 0,5 und y₀ = 0,1

x_o = 0,1 und y₀ = 0,12

Wird a vergrößert (a = 0,015) dann entstehen wieder komplexere Strukturen.

Die folgende Abbildungen zeigt das Ergebnis für verschiedene Startwerte, liegen die Punkte auf der Diagonalen werden die Startwerte blau gefärbt, sind sie symmetrisch werden sie rot gefärbt, sind sie asymmetrisch werden sie grün gefärbt (2 Varianten).

a = 0,0 und b = 3,5    4 Millionen Punkte

a = 0,02 und b = 3,5    4 Millionen Punkte

a = 0,035 und b = 3,5    4 Millionen Punkte

a = 0,045 und b = 3,65    4 Millionen Punkte

x_o = 0,3 und y₀ = 0,1

Bei a = 0 und b = 3,2 besteht die Struktur nur aus 2 Punkten. Je nach Startwert haben die Punkte eine andere Symmetrie, davon gibt es 2 Varianten.

x_o = 0,1 und y₀ = 0,1

x_o = 0,2 und y₀ = 0,1

Die folgende Abbildungen zeigt das Ergebnis für verschiedene Startwerte, liegen die Punkte nicht auf der Diagonalen werden die Startwerte blau gefärbt.

a = 0 und b = 3,2

a = 0,02 und b = 3,2

a = 0,03 und b = 3,2    16 Millionen Punkte

a = 0,03 und b = 3,2    Ausschnitt X,y = 0 bis 0,2    16 Millionen Punkte

a = 0,06 und b = 3,2    16 Millionen Punkte

Bei a = 0 und b = 3,65 gibt es wieder komplexere Strukturen

x_o = 0,1 und y₀ = 0,1

x_o = 0,2 und y₀ = 0,1

x_o = 0,3 und y₀ = 0,1

x_o = 0,95 und y₀ = 0,25

x_o = 0,95 und y₀ = 0,50

Bei a = 0,1018 und b = 3,7 gibt es 4 verschiedene Zustände. Je nach Startwert haben die Punkte eine andere Symmetrie, sie liegen auf der Diagonalen, sie bilden 12 Tori, sie bilden 4 symmetrische Punkte oder sie bilden 2 symmetrische Punkte.

x_o = 0,1 und y₀ = 0,1

x_o = 0,2 und y₀ = 0,1

x_o = 0,3 und y₀ = 0,1

x_o = 0,4 und y₀ = 0,1

Die folgende Abbildungen zeigt das Ergebnis für verschiedene Startwerte, liegen die Punkte auf der Diagonalen werden die Startwerte blau gefärbt, sind sie symmetrisch (2 Punkte) werden sie rot gefärbt, sind sie symmetrisch (4 Punkte) werden sie hellgrün gefärbt und bei Tori dunkelgrün.

a = 0,1018 und b = 3,7    4 Millionen Punkte

Das Bifurkationsdiagramm für a = 0,0 und b = 0,0 - 4,0 mit x_o = 0,3 und y₀ = 0,1.

Das Bifurkationsdiagramm für a = 1,1 und b = 0,0 - 4,0 mit x_o = 0,3 und y₀ = 0,1.

Ausschnitt: b = 3,17 - 3,58

Ausschnitt: b = 3,20 - 3,26

Ausschnitt: b = 3,38 - 3,56

Zum Schluß noch ein paar interessante Maps mit x_o = 0,3 und y₀ = 0,1.

a = 1,1 und b = 3,54    10 Millionen Punkte

a = 1,1 und b = 3,54    Ausschnitt mit 100 Millionen Punkten

Eine ähnliche Struktur erhält man bei a = 1,4 und b = 3,0. Der Winkel des "Daches" beträgt 120°.

a = 1,4 und b = 3,0    Ausschnitt mit 50 Millionen Punkten

Schon kleine Veränderungen der Konstante b verändert die Map.

a = 1,1

         b = 3,450 : vier Punkte (grün)
         b = 3,456 : vier Tori (rot)
         b = 3,470 : vier mal 9 Tori (blau)

Das Plugin zur Erzeugung des Attraktors (für Cinema Version 11) kann auf der Download Seite runtergeladen werden.

[zurück]

[Inhaltsverzeichnis]

[vor]