| [zurück] | Spiraltorus |
[vor] |
Zum Schluß möchte ich noch kurz auf den Spiraltorus (oder die Kreishelix) eingehen dessen Formel schon von Thomas Hendorfer im Forum vorgestellt wurde.
|
X(t) = R * cos(t * pi) + cos(t * pi) * r * cos(n * t * pi) |
2-54 |
|
|
Y(t) = r * sin(n * t * pi) |
2-55 |
|
|
Z(t) = R * sin(t * pi) + sin(t * pi) * r * cos(n * t * pi) |
2-56 |
Die Konstanten haben folgende Bedeutung.
|
R |
: Radius des Kreises |
|
|
r |
: Radius der Spirale |
|
|
N |
: Anzahl Windungen |
Solche Spiralen werden in der Technik z.B. zur Verstärkung von Dichtungsringen eingesetzt. Die Windungen liegen dabei so dicht zusammen das sich die Drähte auf der Innenseite berühren. Um dieses Aussehen zu erreichen müssen wir die Anzahl der Windungen entsprechend erhöhen. Damit die Spirale noch rund aussieht muß der Faktor dt sehr klein sein. In Cinema ist es aber nicht möglich kleinere Werte als dt = 0.001 einzugeben. Für sehr große Werte von n ist das zuwenig und die Spirale sieht eckig aus. Deshalb sollte auch die Splineart von Linear auf Kubisch geändert werden bevor das Schlauchobjekt erzeugt wird.
In Cinema geben wir folgendes ein.
|
X(t) |
: |
cos(1*t*pi) * 200 + cos(t*pi) * 50 * cos(100*t*pi) |
|
|
Y(t) |
: |
50 * sin(100*t*pi) |
|
|
Z(t) |
: |
sin(1*t*pi) * 200 + sin(t*pi) * 50 * cos(100*t*pi) |
|
|
t-Min |
: |
0 |
|
|
t-Max |
: |
2 |
|
|
dt |
: |
0.001 |
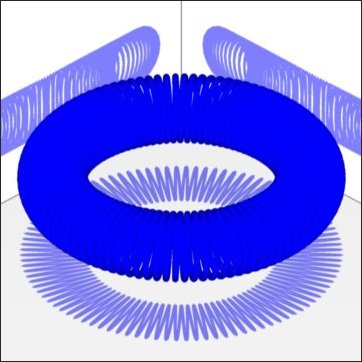
Abb. 2-9
| [zurück] | [Inhaltsverzeichnis] | [vor] |