| [zurück] | Doppelspirale |
Aus dem Spiraltorus können wir einfach eine Doppelspirale machen. Wir addieren zur Funktion Y(t) eine lineare Steigung.
In Cinema geben wir folgendes ein.
|
X(t) |
: |
cos(1*t*pi) * 200 + cos(t*pi) * 80 * cos(25*t*pi) |
|
|
Y(t) |
: |
80 * sin(25*t*pi) + 120 *t |
|
|
Z(t) |
: |
sin(1*t*pi) * 200 + sin(t*pi) * 80 * cos(25*t*pi) |
|
|
t-Min |
: |
0 |
|
|
t-Max |
: |
4 |
|
|
dt |
: |
0.001 |
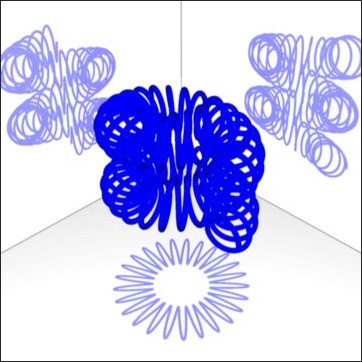
Abb. 2-10a
Diese Doppelspirale können wir als Basis für eine technisch sinnvolle Spirale aus zwei tordierten Drähten verwenden. Dazu werden zwei identische Objekte erzeugt die gegeneinander verdreht und verschoben werden.
|
X(t) = cos(t*pi) * R + cos(t*pi) * D * cos(N*t*pi) |
2-57 |
|
|
Y(t) = D * sin(N*t*pi) + 0.5 * G *t |
2-58 |
|
|
Z(t) = sin(t*pi) * R + sin(t*pi) * D * cos(N*t*pi) |
2-59 |
|
R |
: |
Radius der Spirale |
|
|
G |
: |
Ganghöhe der Spirale (Höhe einer Umdrehung) |
|
|
D |
: |
Radius des Drahtes |
|
|
N |
: |
Anzahl Windungen des Drahtes pro Umdrehung |
|
|
Alpha |
: |
Winkeldifferenz der beiden Drähte |
|
|
DY |
: |
Höhendifferenz der beiden Drähte |
Die Parameter Alpha und DY lassen sich aus den anderen Konstanten berechnen.
|
Alpha = 180 / N |
2-60 |
|
|
DY = 0.5 * G / N |
2-61 |
Wir wählen folgende Konstanten.
|
R |
: |
100 |
|
|
G |
: |
160 |
|
|
D |
: |
5 |
|
|
N |
: |
10 |
Für die Parameter Alpha und DY erhalten wir.
|
Alpha |
: |
18 |
|
|
DY |
: |
8 |
In Cinema geben wir folgendes ein.
|
X(t) |
: |
cos(1*t*pi) * 100 + cos(t*pi) * 5 * cos(10*t*pi) |
|
|
Y(t) |
: |
5 * sin(10*t*pi) + 80 *t |
|
|
Z(t) |
: |
sin(1*t*pi) * 100 + sin(t*pi) * 5 * cos(10*t*pi) |
|
|
t-Min |
: |
0 |
|
|
t-Max |
: |
6 |
|
|
dt |
: |
0.001 |
Aus der so erzeugten Splinekurve machen wir zwei identische Schlauchobjekte. Um die beiden Schlauchobjekte besser zu unterscheiden geben wir ihnen verschiedene Farben. Jetzt verdrehen wir eines der beiden Objekte um den Winkel H = Alpha und verschieben ihn um den Wert DY nach oben (Y-Achse).

Abb. 2-10b
Die Anzahl der Windungen läßt sich bei vorgegebenem Drahtradius nicht beliebig erhöhen. Irgendwann stoßen die Drahtwindungen aneinander. Die maximale Anzahl der Windungen läßt sich leicht berechnen.
|
N-Max = 180 / D |
2-62 |
Für die nächste Spirale wählen wir folgende Konstanten.
|
R |
: |
120 |
|
|
G |
: |
200 |
|
|
D |
: |
10 |
|
|
N |
: |
18 |
|
|
Alpha |
: |
10 |
|
|
DY |
: |
5.5555 |
In Cinema geben wir folgendes ein.
|
X(t) |
: |
cos(t*pi) * 120 + cos(t*pi) * 10 * cos(18*t*pi) |
|
|
Y(t) |
: |
10 * sin(18*t*pi) + 0.5 * 200 *t |
|
|
Z(t) |
: |
sin(t*pi) * 120 + sin(t*pi) * 10 * cos(18*t*pi) |
|
|
t-Min |
: |
0 |
|
|
t-Max |
: |
4 |
|
|
dt |
: |
0.001 |
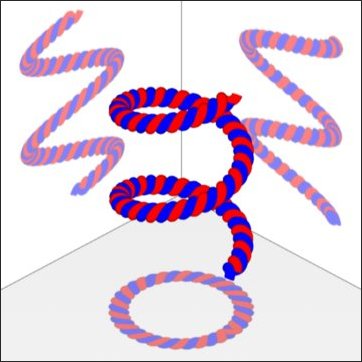
Abb. 2-10c
(c) Jürgen Meier
| [zurück] | [Inhaltsverzeichnis] |