| [zurück] | Kugelspirale |
[vor] |
Die Parameterdarstellung der in der Literatur beschriebenen Kugelspirale lautet.
|
X(t) = cos(t) * cos(arctan(a * t)) |
2-51 |
|
|
Y(t) = sin(t) * cos(arctan(a * t)) |
2-52 |
|
|
Z(t) = - sin(arctan(a * t)) |
2-53 |
Um eine Spirale mit einer Höhe vom 400 mm in Richtung der Y Achse zu erzeugen müssen wir die Funktionen etwas umstellen und ergänzen. Dabei ist zu beachten das die Funktion arctan(t) in Cinema atan(t) heißt.
Wir wählen als Konstante a = 0.15.
In Cinema geben wir folgendes ein.
|
X(t) |
: |
200 * cos(t) * cos(atan(0.15 * t)) |
|
|
Y(t) |
: |
- 200 * sin(atan(0.15 * t)) |
|
|
Z(t) |
: |
200 * sin(t) * cos(atan(0.15 * t)) |
|
|
t-Min |
: |
-35 |
|
|
t-Max |
: |
35 |
|
|
dt |
: |
0.1 |
Um die Symmetrie zu verdeutlichen wurden in Abb. 2-8 drei Kreise eingeblendet. Die Spirale windet sich von Pol zu Pol um eine Kugel.
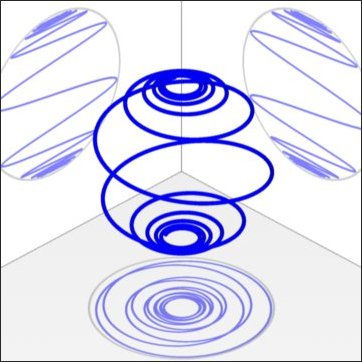
Abb. 2-8
| [zurück] | [Inhaltsverzeichnis] | [vor] |