| [zurück] | Beispiel 7 (Sofafedern) |
[vor] |
Wir wollen jetzt die Spiralfeder aus Beispiel 6 so umformen das die Windungen zu den Enden hin enger zusammenlaufen, ähnlich wie in Beispiel 5. Wir benutzen auch diesmal die Hyperbolische Tangensfunktion Gl. 2-25.
|
Y(t) = a * tanh(b * t) |
Damit sich die beiden letzten Windungen berühren muß ihre Abstand gleich dem Drahtdurchmesser sein. Daraus ergeben sich folgende Randbedingungen.
|
Y(0) = 0 |
2-39 |
|
|
Y(8) = 190 |
2-40 |
|
|
Y(10) = 200 |
2-41 |
Wie in Beispiel 5 ermitteln wir die Konstanten a und b.
|
b = 0.1896 |
||
|
a = 209.22 |
In Cinema geben wir folgendes ein.
|
X(t) |
: |
sqrt(10000 - 100 * t*t) * sin(t * pi) |
|
|
Y(t) |
: |
209.22 * tanh(0.1896 * t) |
|
|
Z(t) |
: |
sqrt(10000 - 100 * t*t) * cos(t * pi) |
|
|
t-Min |
: |
-10 |
|
|
t-Max |
: |
10 |
|
|
dt |
: |
0.01 |
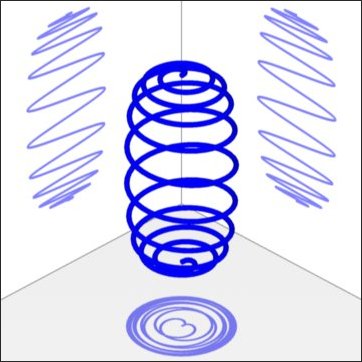
Abb. 2-7a
Das Ergebnis ist noch nicht so befriedigend. Die Form der Feder ist zu zylindrisch und die Anzahl der Windungen in der Mitte ist zu hoch.
Um die Feder etwas bauchiger zu gestalten benutzen wir zur Skalierung des Radius eine andere Funktion. Statt der Ellipse nehmen wir die Cosinusfunktion.
|
r(t) = cos(t * pi) |
2-42 |
Da wir keine periodisch verformte Feder haben wollen dürfen wir nur eine halbe Periode der Funktion benutzen. Die Cosinusfunktion ist symmetrisch zum Koordinatenursprung, daraus ergeben sich folgende Randbedingungen.
|
cos(0.5 * pi) = 0 |
2-43 |
|
|
cos(0.0 * pi) = 1 |
2-44 |
|
|
cos(-0.5 * pi) = 0 |
2-45 |
Da der Definitionsbereich des Parameters t größer ist müssen wir die Funktion leicht modifizieren und fügen zwei Konstanten a und b ein.
|
r(t) = a * cos(b * t * pi) |
2-46 |
Mit der Konstanten a bestimmen wir den Durchmesser der Feder in der Mitte. Die Konstante b ergibt sich aus dem Definitionsbereich des Parameters t. Sie beträgt b = 0.05.
Mit dieser Funktion wollen wird den Radius der Spirale skalieren.
|
r(t) = 200 * cos(0.05 * t * pi) |
2-47 |
In Cinema geben wir folgendes ein.
|
X(t) |
: |
200 * cos(0.05 * t * pi) * sin(t * pi) |
|
|
Y(t) |
: |
209.22 * tanh(0.1896 * t) |
|
|
Z(t) |
: |
200 * cos(0.05 * t * pi) * cos(t * pi) |
|
|
t-Min |
: |
-10 |
|
|
t-Max |
: |
10 |
|
|
dt |
: |
0.01 |
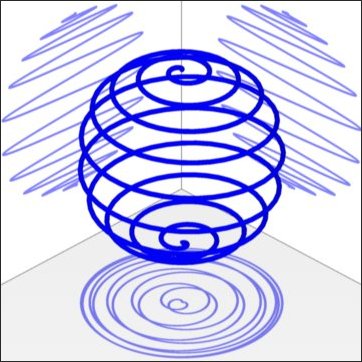
Abb. 2-7b
Diese Feder sieht schon etwas bauchiger aus. Um den Effekt zu verbesserrn versuchen wir es einmal mit der Glockenkurve (siehe Gleichung 1-58 im Tutorial Teil 1).
|
Y = b * exp( -(a * x)2) |
Mit dieser Funktion wollen wir den Radius der Spirale skalieren. Wir wählen die Konstanten a = 0,2 und b = 200.
|
r(t) = 200 * exp(-((0.2 * t)^2)) |
2-48 |
Um in der Mitte weniger Windungen zu bekommen müssen wir auch die Funktion Y(t) modifizieren.
|
Y(t) = 201,0 * tanh(0.3 * t) |
2-49 |
In Cinema geben wir folgendes ein.
|
X(t) |
: |
200 * exp(-((0.2 * t)^2)) * sin(t * pi) |
|
|
Y(t) |
: |
201.0 * tanh(0.3 * t) |
|
|
Z(t) |
: |
200 * exp(-((0.2 * t)^2)) * cos(t * pi) |
|
|
t-Min |
: |
-10 |
|
|
t-Max |
: |
10 |
|
|
dt |
: |
0.01 |
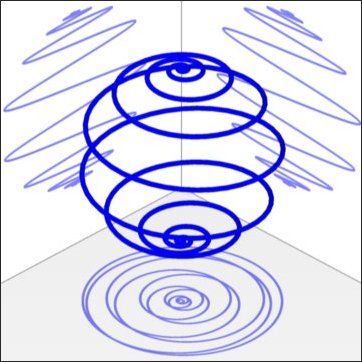
Abb. 2-7c
Wir haben eine Spiralfeder die sich prima als Sofafeder eignet. Als Polsterfedern werden auch konkav geformte Federn verwendet. Die Feder soll in der Mitte einen geringeren Durchmesser als an den Enden haben. Dazu müssen wir Gleichung 2-48 etwas modifizieren.
|
r(t) = (200 - 150 * exp(-((0.2 * t)^2))) |
2-50 |
Die Funktion Y(t) verändern wir solange bis wir ein ansprechendes Ergebnis erhalten.
In Cinema geben wir folgendes ein.
|
X(t) |
: |
(200 - 140 * exp(-((0.2 * t)^2))) * sin(t * pi) |
|
|
Y(t) |
: |
207.46 * tanh(0.2 * t) |
|
|
Z(t) |
: |
(200 - 140 * exp(-((0.2 * t)^2))) * cos(t * pi) |
|
|
t-Min |
: |
-10 |
|
|
t-Max |
: |
10 |
|
|
dt |
: |
0.01 |
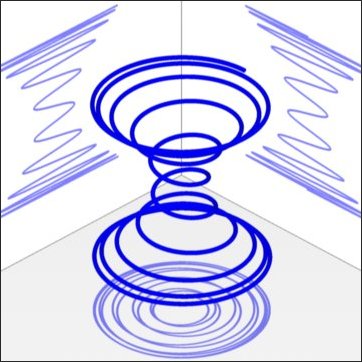
Abb. 2-7d
| [zurück] | [Inhaltsverzeichnis] | [vor] |