| [zurück] | Beispiel 4 (verformte Spiralfeder Teil 2) |
[vor] |
Der verbogene Anfang der Spirale hat seine Ursache in der starken Steigung der Exponentialfunktion bei sehr kleinen Werten von t. Deshalb knipsen wir einfach unten eine Windung der Spirale ab und fügen oben zusätzlich eine Windung an. Dazu brauchen wir nur den Definitionsbereich des Parameters t zu verändern.
|
t-Min |
: |
1 |
|
|
t-Max |
: |
21 |
|
|
dt |
: |
0.01 |
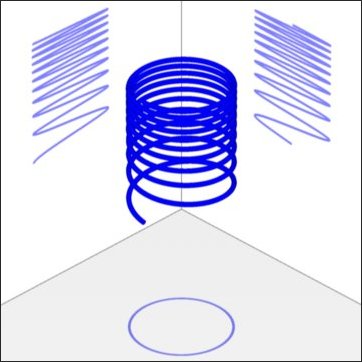
Abb. 2-4a
Die Spiralfeder hat nun am Anfang die gewünschte Steigung. Durch diese Veränderung haben wir aber die Spiralfeder entlang der Y Achse skaliert und nach oben verschoben, sie ist jetzt nur noch 267 mm hoch.
|
Y(t) = 140.2 * t ^ 0,35 |
2-13 |
|
|
Y(1) = 140,2 |
2-14 |
|
|
Y(21) = 406,9 |
2-15 |
Diese Skalierung müssen wir vermeiden und die Funktion Y(t) neu berechnen. Wir berechnen die Werte erneut ohne Multiplikator.
|
Y(t) = t ^ 0,35 |
2-16 |
|
|
Y(1) = 1 |
2-17 |
|
|
Y(21) = 2,90 |
2-18 |
Damit die Spiralfeder wieder ihre ursprünglichen Maße bekommt muß die Funktion Y(t) aber folgende Bedingungen erfüllen.
|
Y(1) = 0 |
2-19 |
|
|
Y(21) = 400 |
2-20 |
Die erste Bedingung (Gl. 2-19) läßt sich leicht erfüllen.
|
Y(t) = t ^ 0.35 – 1 |
2-21 |
|
|
Y(1) = 0 |
2-22 |
|
|
Y(21) = 1.90 |
2-23 |
Um die zweite Bedingung (Gl. 2-20) zu erfüllen müssen wir wieder einen Multiplikator 400/1,9 = 210,25 einführen. Die gesuchte Funktion lautet.
|
Y(t) = 210.25 * (t ^ 0.35 – 1) |
2-24 |
Wir ergänzen die Formel in Cinema.
|
X(t) |
: |
100 * sin(t * pi) |
|
|
Y(t) |
: |
210.25 * (t ^ 0.35 – 1) |
|
|
Z(t) |
: |
100 * cos(t * pi) |
|
|
t-Min |
: |
1 |
|
|
t-Max |
: |
21 |
|
|
dt |
: |
0.01 |
Damit hat die Spiralfeder jetzt das gewünschte Aussehen und die korrekten Maße.

Abb. 2-4b
| [zurück] | [Inhaltsverzeichnis] | [vor] |