| [zurück] | Beispiel 2 (konische Spiralfeder) |
[vor] |
Jetzt wollen wir aus der zylinderförmigen Spiralfeder eine kegelförmige Feder machen. Oben soll der Durchmesser nicht mehr 200 mm sondern nur noch 50 mm betragen. Um dies zu erreichen müssen wird den Radius der Kreisfunktion entsprechend skalieren.
Die Funktion r(t) muß dabei folgende Bedingungen erfüllen.
|
r(0) = 100 |
2-1 |
|
|
r(20) = 25 |
2-2 |
Bei t = 0 beträgt der Radius 100 mm, bei t = 20 beträgt er 25 mm. Wir haben wieder einen linearen Zusammenhang (Gerade, y = a * x + b) und die gesuchte Funktion r(t) läßt sich aus den beiden Wertepaaren berechnen. Dazu benutzen wir die Zweipunktform der Geradengleichung.
|
(r – r1)/(t – t1) = (r2 – r1)/(t2 – t1) |
2-3 |
Wenn wird die beiden Wertepaare (Gl. 2-1/2) in die Gleichung einsetzen erhalten wir.
|
(r – 100)/(t – 0) = (25 – 100)/(20 – 0) |
2-4 |
Diese Gleichung läßt sich problemlos nach r auflösen und so erhalten wir die gewünschte Funktion.
|
r(t) = -3.75 * t + 100 |
2-5 |
Diese Funktion setzen wir an Stelle der Konstanten 100 in die Kreisfunktion ein
|
X(t) |
: |
(-3.75 * t + 100) * sin(t * pi) |
|
|
Y(t) |
: |
20 * t |
|
|
Z(t) |
: |
(-3.75 * t + 100) * cos(t * pi) |
und wir erhalten die gewünschte kegelförmige Spiralfeder.
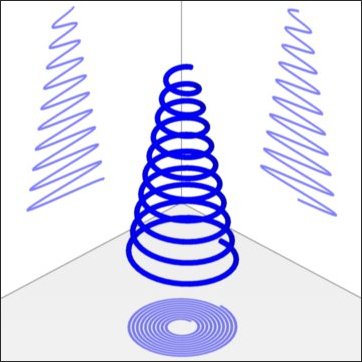
Abb. 2-2
| [zurück] | [Inhaltsverzeichnis] | [vor] |