| [zurück] | 2.3. Zylinder-Zylinder III |
[vor] |
Jetzt wird es richtig kompliziert, wir nehmen zwei Zylinder und verdrehen sie um den Winkel ß. Die Idee zu diesem Tutorial sowie ein Teil der folgenden Gleichungen stammen aus einer Veröffentlichung von Prof. John M. Stockie [6].
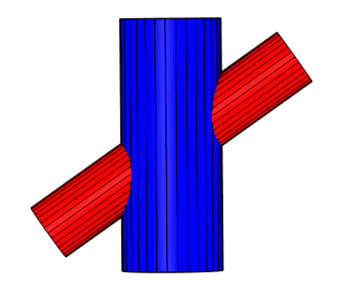
Abb. 28
Da wir bei der Herleitung der Formeln mit Matrizen arbeiten schreiben wir die Zylindergleichungen als Vektor. Abb. 28 zeigt die beiden Zylinder in der x,z-Ebene. Die Gleichung des ersten Zylinders lautet.
|
|
9-38 |
Der zweite Zylinder ist gegenüber dem ersten Zylinder um den Winkel ß verdreht. Wir multiplizieren die Gleichungen des ersten Zylinders (Gl. 9-38) mit der folgenden Rotationsmatrix.
|
|
9-39 |
|
|
9-40 |
Dabei ändern wir den Index der Parameter u und v von 1 auf 2. So erhalten wir die Gleichungen für den zweiten Zylinder.
|
|
9-41 |
Wie bei den bisherigen Beispielen müssen wir beide Gleichungen (9-38 und 9-41) gleichsetzen.
|
|
9-42 |
Wir lösen Gl. 9-43 nach sin(u1) auf.
|
|
9-45 |
Daraus bilden wir mit Hilfe von Gl. 9-11 den Cosinus.
|
|
9-46 |
Jetzt setzen wir Gl. 9-46 in Gl. 9-42 ein.
|
|
9-47 |
Wir vereinfachen Gl. 9-47 ein wenig und lösen sie nach v2 auf.
|
|
9-48 |
|
|
9-49 |
|
|
9-50 |
Jetzt setzen wir Gl. 9-50 in Gl. 9-44 ein und erhalten für v1.
|
|
9-51 |
Jetzt setzen wir geschickt die gewonnenen Formeln in die Gleichung zur Erzeugung des ersten Zylinders ein. Zuerst setzten wir Gl. 9-46 in Gl. 9-38 ein.
|
|
9-52 |
Dann setzten wir Gl. 9-45 in Gl. 9-38 ein.
|
|
9-53 |
Zuletzt setzten wir Gl. 9-51 in Gl. 9-38 ein.
|
|
9-54 |
Jetzt haben wir für x, y und z Gleichungen die nur noch den Parameter u2 enthalten. Wir ersetzten u2 durch den Parameter t und erhalten die gewünschten Formeln für die Schnittlinie. Da es ja zwei Schnittlinien gibt erhalten wir auch zwei Gleichungen.
|
|
9-55 |
|
|
9-56 |
Wenn wir diese Gleichungen (Gl. 9-55 und 9-56) mit den Gleichungen (Gl. 9-57 und 9-58) aus dem Artikel [6] vergleichen stellen wir erhebliche Abweichungen fest. Trotzdem sind beide Gleichungen korrekt.
|
|
9-57 |
|
|
9-58 |
Die Gl. 9-57 und 9-58 wurden vom Mathematikprogramm Maple [7,8] erzeugt. Um zu beweisen das beide Lösungen identisch sind setzten wir x(t) aus den Gl. 9-55 und 9-57 gleich.
|
|
9-59 |
Gl. 9-59 stellen wir ein bischen um.
|
|
9-60 |
Gl. 9-64 ist korrekt was uns jede Formelsammlung [1,2] bestätigen kann. Damit ist die Gleichheit bewiesen.
| [zurück] | [Inhaltsverzeichnis] | [vor] |