[zurück]

Zylinder-Zylinder IIa

[vor]

Jetzt müssen wir uns noch um den Fall a > R₁ - R₂ kümmern.

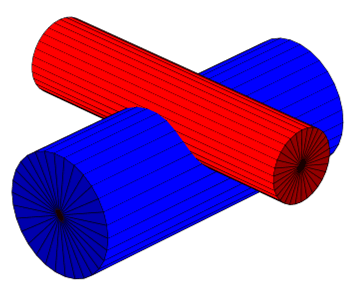
Abb. 20

Dafür habe ich leider keine elegante Lösung gefunden. Zuerst betrachten wir noch einmal die Gleichungen für die Schnittlinie.

Für das Beispiel R₁ = 50 und R₂ = 30 berechnen wir die Kurve für verschiedene Werte von a (a = 20, 40, 60, 70 von links nach rechts). Berechnet werden 48 Punkte. Abb. 21 zeigt die perspektivische Darstellung.

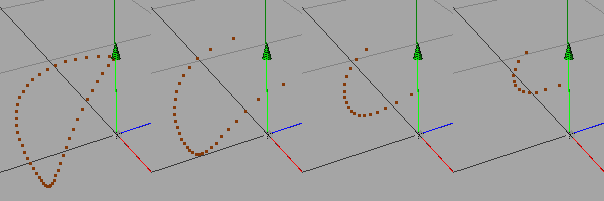
Abb. 21

Abb. 22 zeigt die Seitenansicht vom Ende des Zweiten Zylinders (R₂) aus gesehen. Für a = 20 erhalten wir einen vollen Kreis, alle Punkte haben den gleichen Abstand. Für größere Werte von a existiert keine Schnittlinie mehr im oberen Bereich des Zylinders und die Wurzel aus Gl. 9-29 wird negativ.

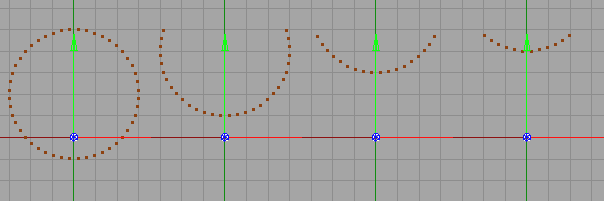
Abb. 22

Abb. 23 zeigt die Draufsicht.

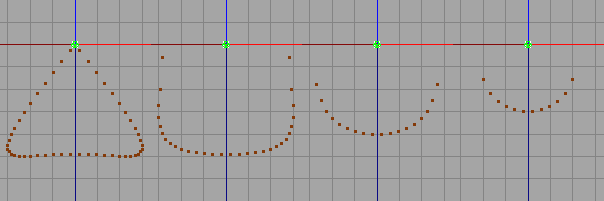
Abb. 23

Je größer a wird desto größer werden die Abstände der Punkte wenn wir uns der Mitte von Zylinder 1 nähern. Die Berechnung erfolgt über den Parameter von Zylinder 2 (u₂). Wir können die Berechnung auch über den Parameter von Zylinder 1 durchführen (u₁).
Dazu betrachten wir wieder die Gl. 9-7/21/9 auf Seite 5.
Wir lösen Gl. 9-21 nach sin(u₁) auf und bilden daraus cos(u₁).

Die so gewonnenen Formeln setzen wir in die Gleichung des 2. Zylinders ein. Den Parameter u₁ ersetzten wir wieder durch t und erhalten.

Sowohl die Gl. 27/28/29 als auch Gl. 35/36/37 beschreiben die gleiche Schnittlinie, nur die Verteilung der Punkte bei der Berechnung ist anders.
Um ein brauchbares Ergebnis für die Schnittlinie zu bekommen müßte man beide Gleichungen kombinieren, darauf habe ich im Moment verzichtet.

Um diese Problematik zu verstehen am besten ein bischen mit dem Plugin spielen. Mit viel Handarbeit kann man aber auch damit ein brauchbares Ergebnis erzielen (siehe nächste Seite).

[zurück]

[Inhaltsverzeichnis]

[vor]