| [zurück] | 2.5. Basketball |
[vor] |
Ein Basketball hat auf seiner Oberfläche eine charakteristische Zeichnung. Diese läßt sich einfach mathematisch durch die Schnittlinie zwischen einer Kugel und einem hyperbolischen Paraboloid ausdrücken.
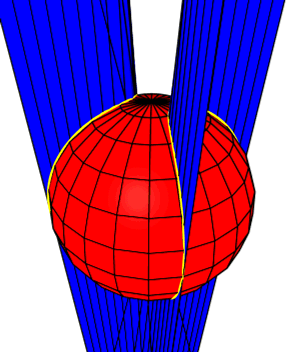
Abb. 52
Zuerst nehmen wir eine Kugel mit dem Radius r.
|
x = r cos(u1) sin(v1) |
9-110 |
|
|
y = r sin(u1) sin(v1) |
9-111 |
|
|
z = r cos(v1) |
9-112 |
Für den hyperbolischen Paraboloid modifizieren wir die Gl. 3-287/288/289 ein bischen indem wir den Faktor a hinzufügen und 2 Achsen vertauschen.
|
x = a u2 |
9-113 |
|
|
y = a u2 v2 |
9-114 |
|
|
z = a v2 |
9-115 |
Für die Schnittlinie müssen wir wieder beide Gleichungen gleichsetzen.
|
r cos(u1) sin(v1) = a u2 |
9-116 |
|
|
r sin(u1) sin(v1) = a u2 v2 |
9-117 |
|
|
r cos(v1) = a v2 |
9-118 |
Zuerst lösen wir Gl. 9-116 nach u2 auf.
|
u2 = (r cos(u1) sin(v1))/a |
9-119 |
Dann lösen wir Gl. 9-118 nach v2 auf.
|
v2 = (r cos(v1))/a |
9-120 |
Jetzt setzen wir Gl. 9-119 und Gl. 9-120 in Gl. 9-117 ein.
|
|
9-121 |
Gl. 9-121 lösen wir schrittweise nach u1 auf.
|
|
9-122 |
|
|
|
9-123 |
|
|
|
9-124 |
|
|
|
9-125 |
Gl. 9-125 setzen wir in Gl. 9-110 und Gl. 9-111 ein.
|
|
9-126 |
|
|
|
9-127 |
Den Parameter v1 in Gl. 9-126 und 9-127 ersetzen wir durch t und erhalten so zusammen mit Gl. 9-112 die gewünschte Funktion für die Schnittlinie t[0, 2 pi].
|
|
9-128 |
Aus diesen Gleichungen machen wir ein Sweep-NURBS.

Abb. 53
Da sieht nicht besonders spektakulär aus, aber wenn wir eine Kugel und zwei weitere Linien hinzufügen erkennen wir einen Basketball.
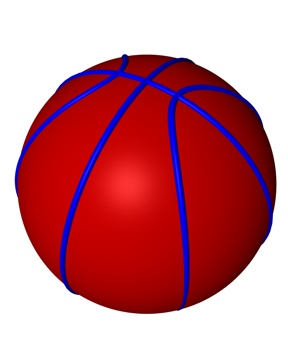
Abb. 54
| [zurück] | [Inhaltsverzeichnis] | [vor] |