| [zurück] | Aufgabe 72 |
[vor] |
![]()
 (Gl. 1)
(Gl. 1)
t ist eine positive ganze Zahl.
![]()
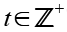 (Gl. 2)
(Gl. 2)
Es gilt.
![]()
 (Gl. 3)
(Gl. 3)
Mit Hilfe von Gl. 3 erhalten wir aus Gl. 1.
![]()
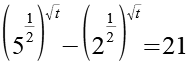 (Gl. 4)
(Gl. 4)
Es gilt.
![]()
 (Gl. 5)
(Gl. 5)
Mit Hilfe von Gl. 5 erhalten wir aus Gl. 4.
![]()
 (Gl. 6)
(Gl. 6)
Den Exponent substituieren wir mit u.
![]()
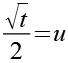 (Gl. 7)
(Gl. 7)
Wir setzen Gl. 7 in Gl. 6 ein.
![]()
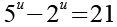 (Gl. 8)
(Gl. 8)
Wir fügen zusätzlich den Exponenten 1 ein.
![]()
 (Gl. 9)
(Gl. 9)
Die 1 ersetzen wir durch folgendes Konstrukt.
![]()
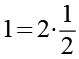 (Gl. 10)
(Gl. 10)
Wir setzen Gl. 10 in Gl. 9 ein.
![]()
 (Gl. 11)
(Gl. 11)
Es gilt.
![]()
 (Gl. 5)
(Gl. 5)
Mit Hilfe von Gl. 5 erhalten wir aus Gl. 11.
![]()
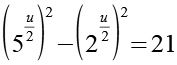 (Gl. 12)
(Gl. 12)
Wir substituieren mit x und y.
![]()
 (Gl. 13)
(Gl. 13)
![]()
 (Gl. 14)
(Gl. 14)
![]()
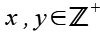 (Gl. 15)
(Gl. 15)
Wir setzen Gl. 13 und Gl. 14 in Gl. 12 ein.
![]()
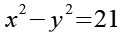 (Gl. 16)
(Gl. 16)
Es gilt.
![]()
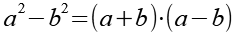 (Gl. 17)
(Gl. 17)
Mit Hilfe von Gl. 17 erhalten wir aus Gl. 16.
![]()
 (Gl. 18)
(Gl. 18)
Da auch x und y positive ganze Zahlen sind gilt.
![]()
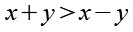 (Gl. 19)
(Gl. 19)
Es gibt 4 verschiedene Möglichkeiten die 21 als Produkt zweier positiver ganzer Zahlen darzustellen.
![]()
 (Gl. 20)
(Gl. 20)
![]()
 (Gl. 21)
(Gl. 21)
![]()
 (Gl. 22)
(Gl. 22)
![]()
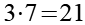 (Gl. 23)
(Gl. 23)
Nach Gl. 19 kommen nur 21*1 und 7*3 als Lösung in Frage. Wir berechnen x und y und prüfen das Ergebnis auf Plausibilität.
 (Gl. 24) (Gl. 24) |
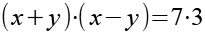 (Gl. 32) (Gl. 32) |
 (Gl. 25) (Gl. 25) |
 (Gl. 33) (Gl. 33) |
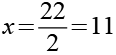 (Gl. 26) (Gl. 26) |
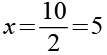 (Gl. 34) (Gl. 34) |
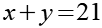 (Gl. 27) (Gl. 27) |
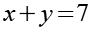 (Gl. 35) (Gl. 35) |
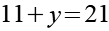 (Gl. 28) (Gl. 28) |
 (Gl. 36) (Gl. 36) |
 (Gl. 29) (Gl. 29) |
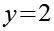 (Gl. 37) (Gl. 37) |
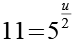 (Gl. 30) (Gl. 30) |
 (Gl. 38) (Gl. 38) |
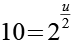 (Gl. 31) (Gl. 31) |
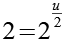 (Gl. 39) (Gl. 39) |
Wie man leicht sehen kann führt nur die zweite Variante (7*3) zu einer sinnvollen Lösung für u.
![]()
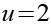 (Gl. 40)
(Gl. 40)
Wir setzen Gl. 40 in Gl. 38 und Gl. 39 ein.
![]()
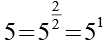 (Gl. 41)
(Gl. 41)
![]()
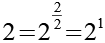 (Gl. 42)
(Gl. 42)
Wir setzen Gl. 40 in Gl. 7 ein.
![]()
 (Gl. 43)
(Gl. 43)
Beide Seiten multiplizieren wir mit 2.
![]()
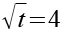 (Gl. 44)
(Gl. 44)
Auf beiden Seiten ziehen wir die Wurzel und erhalten die Lösung für Gl. 1.
![]()
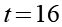 (Gl. 45)
(Gl. 45)
Kontrolle
Zur Kontrolle setzen wir Gl. 45 in Gl. 1 ein.
![]()
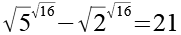 (Gl. 46)
(Gl. 46)
![]()
 (Gl. 47)
(Gl. 47)
![]()
 (Gl. 48)
(Gl. 48)
![]()
 (Gl. 49)
(Gl. 49)
![]()
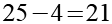 (Gl. 50)
(Gl. 50)
![]()
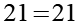 (Gl. 51)
(Gl. 51)
Anhang
![]()
 (Gl. 1)
(Gl. 1)
Die Aufgabe läßt sich natürlich auch durch einfaches Probieren lösen.
| t | |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
0,8219 1,4881 2,2076 3 3,8755 4,8418 5,9055 7,0734 8,3519 9,7479 11,2684 12,9205 14,7117 16,6499 18,7432 21 23,4291 26,0397 28,8412 31,8437 |
| [zurück] | [Inhaltsverzeichnis] | [vor] |