Aufgabe 60
|
[zurück] | Aufgabe 60 |
[vor] | |
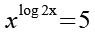(Gl. 1)
Beide Seiten werden logarithmiert.
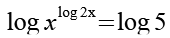(Gl. 2)
Es gilt.
(Gl. 3)
Mit Hilfe von Gl. 3 erhalten wir aus Gl. 2.
(Gl. 4)
Es gilt.
(Gl. 5)
Mit Hilfe von Gl. 5 erhalten wir aus Gl. 4.
(Gl. 6)
Wir substituieren log x durch t.
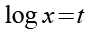(Gl. 7)
Gl. 7 setzen wir i n Gl. 6 ein.
(Gl. 8)
Die Klammer wird ausmultipliziert.
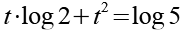(Gl. 9)
Auf beiden Seiten subtrahieren wir log 5.
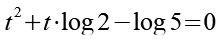(Gl. 10)
Wir ersetzen die 2 durch 10/5.
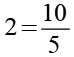(Gl. 11)
Gl. 11 setzen wir in Gl. 10 ein.
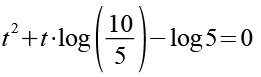(Gl. 12)
Es gilt.
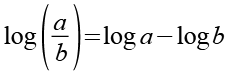(Gl. 13)
Mit Hilfe von Gl. 13 erhalten wir aus Gl. 12.
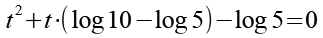(Gl. 14)
Es gilt.
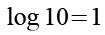(Gl. 15)
Mit Hilfe von Gl. 15 erhalten wir aus Gl. 14. Zum alternativen Lösungsweg siehe Anhang.
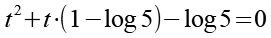(Gl. 16)
Wir multiplizieren die Klammer aus.
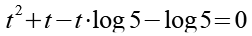(Gl. 17)
Wir können einmal t und einmal log 5 ausklammern.
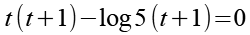(Gl. 18)
Jetzt können wir t+1 ausklammern. Wir erhalten auf der linken Seite ein Produkt deren Teile wir getrennt gleich Null setzen können.
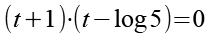(Gl. 19)
Wir setzen die linke Klammer gleich Null.
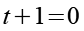(Gl. 20)
Das erste Ergebnis der quadratischen Gleichung.
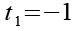(Gl. 21)
Wir setzen die rechte Klammer gleich Null.
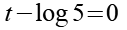(Gl. 22)
Das zweite Ergebnis der quadratischen Gleichung.
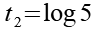(Gl. 23)
Jetzt müssen wir die Substitution wieder rückgängig machen und setzen t1 in Gl. 7 ein.
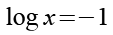(Gl. 24)
Es gilt.
(Gl. 25)
Mit Hilfe von Gl. 25 erhalten wir aus Gl. 24.
(Gl. 26)
Das erste Ergebnis.
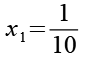(Gl. 27)
Wir setzen t2 in Gl. 7 ein.
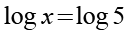(Gl. 28)
Das zweite Ergebnis.
(Gl. 29)
Zur Kontrolle setzen wir x1 in Gl. 1 ein.
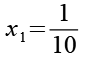(Gl. 27)
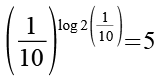(Gl. 30)
(Gl. 31)
Es gilt.
(Gl. 32)
Mit Hilfe von Gl. 32 erhalten wir aus Gl. 31.
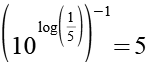(Gl. 33)
Es gilt.
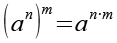(Gl. 34)
Mit Hilfe von Gl. 34 erhalten wir aus Gl. 33.
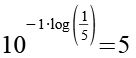(Gl. 35)
Es gilt.
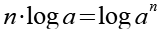(Gl. 36)
Mit Hilfe von Gl. 36 erhalten wir aus Gl. 35.
(Gl. 37)
Es gilt.
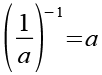(Gl. 38)
Mit Hilfe von Gl. 38 erhalten wir aus Gl. 37.
(Gl. 39)
Mit Hilfe von Gl. 25 erhalten wir aus Gl. 39.
(Gl. 40)
Zur Kontrolle setzen wir x2 in Gl. 1 ein.
(Gl. 29)
(Gl. 42)
(Gl. 43)
Es gilt.
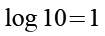(Gl. 44)
Mit Hilfe von Gl. 44 erhalten wir aus Gl. 43.
(Gl. 40)
Anhang
Der klassische Lösungsweg für die quadratische Gleichung.
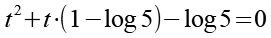(Gl. 16)
Es gilt.
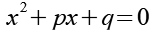(Gl. 45)
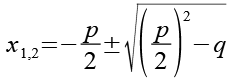(Gl. 46)
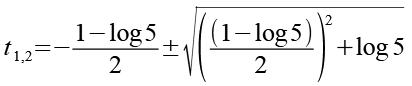(Gl. 47)
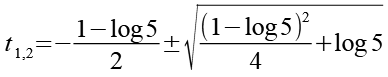(Gl. 48)
Es gilt.
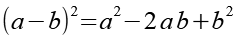(Gl. 49)
Wir wenden Gl. 49 an.
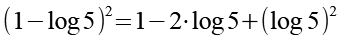(Gl. 50)
Wir setzen Gl. 50 in Gl. 48 ein.
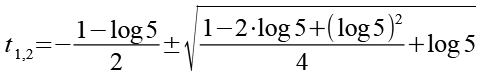(Gl. 51)
Wir bringen beide Brüche auf den gleichen Nenner.
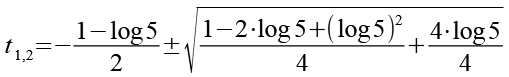(Gl. 52)
Wir fassen beie Brüche zusammen.
(Gl. 53)
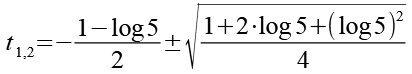(Gl. 54)
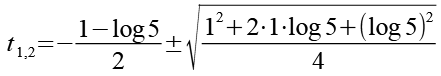(Gl. 55)
Es gilt.
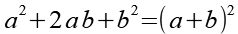(Gl. 56)
Mit Hilfe von Gl. 56 erhalten wir aus Gl. 55.
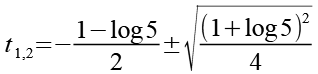(Gl. 57)
Wir ziehen die Wurzel.
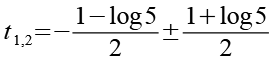(Gl. 58)
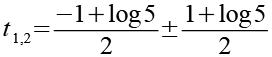(Gl. 59)
Für t1 erhalten wir.
(Gl. 60)
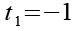(Gl. 21)
Für t2 erhalten wir.
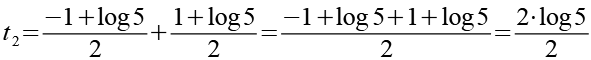(Gl. 61)
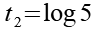(Gl. 23)
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |