[zurück]

Aufgabe 51

[vor]

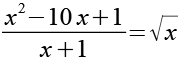      (Gl. 1)

Beide Seiten werden mit (x+1) multipliziert.

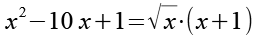      (Gl. 2)

Die Wurzel substituieren wir mit y.

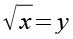      (Gl. 3)

Aus Gl. 3 ergibt sich.

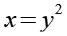      (Gl. 4)

Gl. 3 und Gl. 4 setzen wir in Gl. 2 ein.

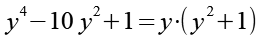      (Gl. 5)

Gl. 5 stellen wir ein bischen um.

      (Gl. 6)

Beide Seiten teilen wir durch y².

      (Gl. 7)

Gl. 7 stellen wir ein bischen um.

      (Gl. 8)

Es gilt.

      (Gl. 9)

a und b drücken wir durch y aus.

      (Gl. 10)  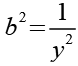     (Gl. 11)

Mit Hilfe von Gl. 10 und Gl. 11 erhalten wir aus Gl. 9.

      (Gl. 12)

Auf der rechten Seite können wir einmal y kürzen.

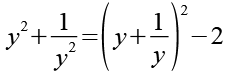      (Gl. 13)

Gl. 13 setzen wir in Gl. 8 ein.

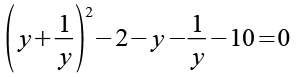      (Gl. 14)

Gl. 14 stellen wir ein bischen um.

      (Gl. 15)

Wir substituieren die Klammer durch t.

      (Gl. 16)

Gl. 16 setzen wir in Gl. 15 ein.

      (Gl. 17)

Für die Lösung der quadratischen Gleichung gilt.

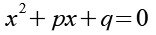      (Gl. 18)

      (Gl. 19)

Für die Lösung von Gl. 17 erhalten wir.

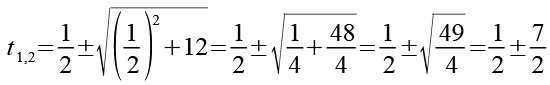      (Gl. 20)

Die beiden Lösungen von Gl. 17.

      (Gl. 21)       (Gl. 22)

Aus t müssen wir y berechnen. Zuerst setzten wir t₁ in Gl. 16 ein.

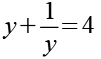      (Gl. 23)

Beide Seiten multiplizieren wir mit y.

      (Gl. 24)

Auf beiden Seiten subtrahieren wir 4y.

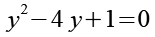      (Gl. 25)

Für die Lösung der quadratischen Gleichung erhalten wir.

      (Gl. 26)

Die beiden Lösungen von Gl. 25.

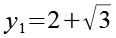      (Gl. 27)  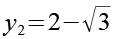     (Gl. 28)

Jetzt setzten wir t₂ in Gl. 16 ein.

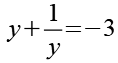      (Gl. 29)

Beide Seiten multiplizieren wir mit y.

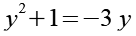      (Gl. 29a)

Auf beiden Seiten subtrahieren wir -3y.

      (Gl. 30)

Für die Lösung der quadratischen Gleichung erhalten wir.

      (Gl. 31)

Die beiden Lösungen von Gl. 30.

      (Gl. 32)       (Gl. 33)

Insgesamt haben wir jetzt 4 Lösungen für y.

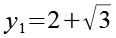      (Gl. 27)  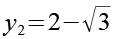     (Gl. 28)       (Gl. 32)       (Gl. 33)

Jetzt müssen wir aus y wieder x berechnen, es gilt.

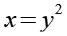      (Gl. 4)

Gl. 27 setzen wir in Gl. 4 ein.

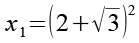      (Gl. 34)

Es gilt.

      (Gl. 35)

Mit Hilfe von Gl. 35 erhalten wir für x₁.

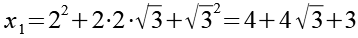      (Gl. 36)

      (Gl. 37)

Gl. 28 setzen wir in Gl. 4 ein.

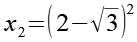      (Gl. 38)

Es gilt.

      (Gl. 39)

Mit Hilfe von Gl. 39 erhalten wir für x₂.

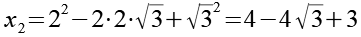      (Gl. 40)

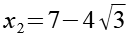      (Gl. 41)

Gl. 32 setzen wir in Gl. 4 ein.

      (Gl. 42)

Mit Hilfe von Gl. 35 erhalten wir für x₃.

      (Gl. 43)

      (Gl. 44)

Gl. 33 setzen wir in Gl. 4 ein.

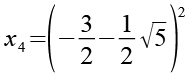      (Gl. 45)

Mit Hilfe von Gl. 39 erhalten wir für x₄.

      (Gl. 46)

      (Gl. 47)

Alle 4 Lösungen für Gl. 1 mit den Zahlenwerten.

      (Gl. 48)  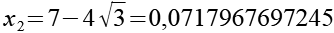     (Gl. 49)       (Gl. 50)       (Gl. 51)

Anhang 1

Gl. 1 können wir auch einfach quadrieren und dann ausmultiplizieren, da führt zu einem Polynom 4. Grades.

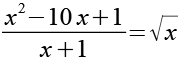      (Gl. 1)

Beide Seiten werden quadriert.

      (Gl. 52)

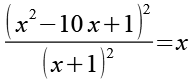      (Gl. 53)

Zähler und Nenner berechnen wir separat.

      (Gl. 54)

      (Gl. 55)

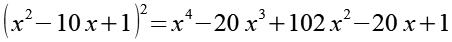      (Gl. 56)

      (Gl. 57)

Gl. 56 und Gl. 57 setzen wir in Gl. 53 ein.

      (Gl. 58)

Beide Seiten multiplizieren wir mit (x²+2x+1).

      (Gl. 59)

      (Gl. 60)

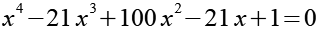      (Gl. 61)

Gl. 61 ist zumindest theoretisch lösbar.

Anhang 2

Wir können Gl. 61 benutzen um die Lösungen x₁ bis x₄ zu überprüfen.

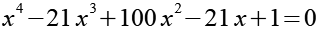      (Gl. 61)

Fangen wir mit x₁ an. Zur besseren Übersicht berechnen wir die Potenzen von x₁ separat.

      (Gl. 37)

x₁²

      (Gl. 62)

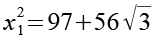      (Gl. 63)

x₁³

Es gilt.

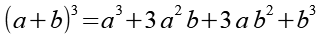      (Gl. 64)

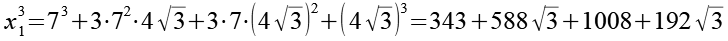      (Gl. 65)

      (Gl. 66)

x₁⁴

Es gilt.

      (Gl. 67)

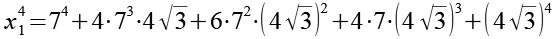      (Gl. 68)

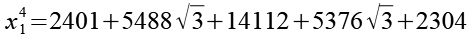      (Gl. 69)

      (Gl. 70)

Jetzt setzen wir Gl. 70, Gl. 66, Gl. 63 und Gl. 37 in Gl. 61 ein.

      (Gl. 71)

      (Gl. 72)

      (Gl. 73)

      (Gl. 74)

Das Ergebnis ist Null, wie es sein soll.

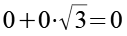      (Gl. 75)

Machen wir mit x₂ weiter.

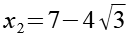      (Gl. 41)

x₂²

      (Gl. 76)

      (Gl. 77)

x₂³

Es gilt.

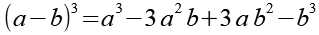      (Gl. 78)

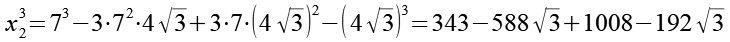      (Gl. 79)

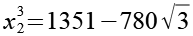      (Gl. 80)

x₂⁴

Es gilt.

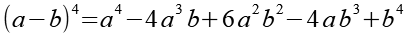      (Gl. 81)

      (Gl. 82)

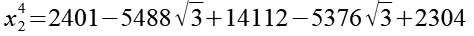      (Gl. 83)

      (Gl. 84)

Jetzt setzen wir Gl. 84, Gl. 80, Gl. 77 und Gl. 41 in Gl. 61 ein.

      (Gl. 85)

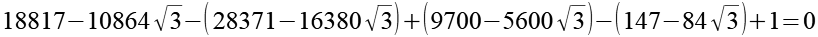      (Gl. 86)

      (Gl. 87)

      (Gl. 88)

Das Ergebnis ist Null, wie es sein soll.

      (Gl. 89)

Machen wir mit x₃ weiter.

      (Gl. 44)

x₃²

      (Gl. 90)

      (Gl. 91)

x₃³

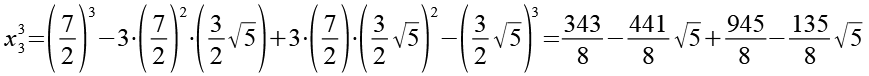      (Gl. 92)

      (Gl. 93)

x₃⁴

      (Gl. 94)

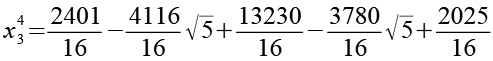      (Gl. 95)

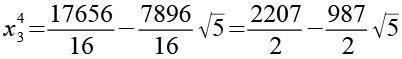      (Gl. 96)

Jetzt setzen wir Gl. 96, Gl. 93, Gl. 91 und Gl. 44 in Gl. 61 ein.

      (Gl. 97)

      (Gl. 98)

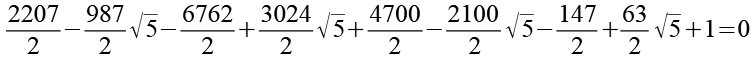      (Gl. 99)

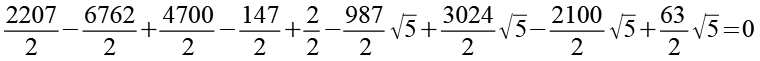      (Gl. 100)

      (Gl. 101)

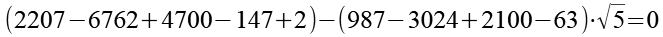      (Gl. 102)

Das Ergebnis ist Null, wie es sein soll.

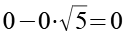      (Gl. 103)

Machen wir mit x₄ weiter.

      (Gl. 47)

x₄²

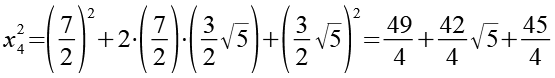      (Gl. 104)

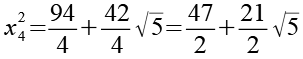      (Gl. 105)

x₄³

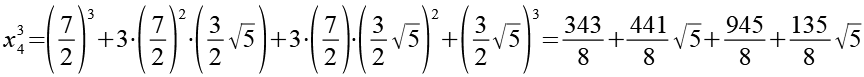      (Gl. 106)

      (Gl. 107)

x₄⁴

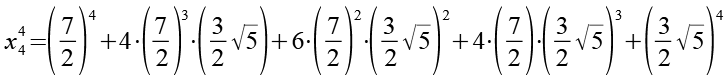      (Gl. 108)

      (Gl. 109)

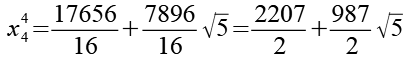      (Gl. 110)

Jetzt setzen wir Gl. 110, Gl. 107, Gl. 105 und Gl. 47 in Gl. 61 ein.

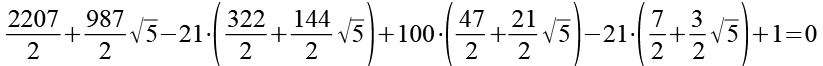      (Gl. 111)

      (Gl. 112)

      (Gl. 113)

      (Gl. 114)

      (Gl. 115)

      (Gl. 116)

Das Ergebnis ist Null, wie es sein soll.

      (Gl. 117)

Anhang 3

      (Gl. 58)

Auch wenn es keinen Sinn macht könnte man den Zähler durch den Nenner teilen.

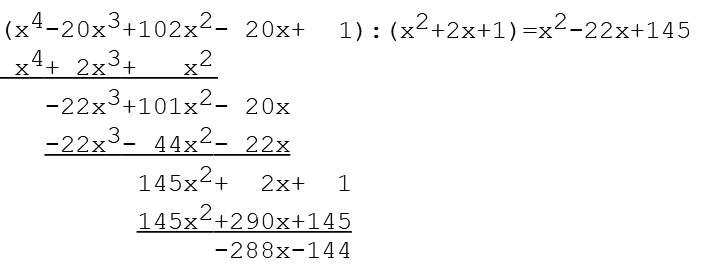
Die Division geht natürlich nicht auf, der Rest ist -288x-144.

[zurück]

[Inhaltsverzeichnis]

[vor]