[zurück]

Aufgabe 49

 [vor]

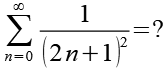      (Gl. 1)

Wir formulieren die ersten Glieder der Folge.

      (Gl. 2)

      (Gl. 3)

Für das Basler Problem gilt.

      (Gl. 4)

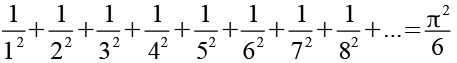      (Gl. 5)

Wir sortieren die Glieder von Gl. 5 nach geraden und ungeraden Zahlen.

      (Gl. 6)

Wir substituieren die beiden Folgen mit S und E.

      (Gl. 7)

Für S erhalten wir.

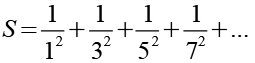      (Gl. 8)

Für S gilt auch Gl. 3.

      (Gl. 9)

Für E erhalten wir.

      (Gl. 10)

Wir können 1/22 ausklammern. Die Folge in der Klammer ist dann mit Gl. 5 identisch.

      (Gl. 11)

Für E erhalten wir dann.

      (Gl. 12)

Gl. 9 und Gl. 12 setzen wir für S und E in Gl. 7 ein.

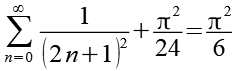      (Gl. 13)

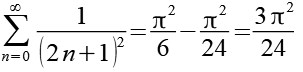      (Gl. 14)

Das Ergebnis.

      (Gl. 15)

Anhang 1

Untersuchen wir die Konvergenz der Folge.

      (Gl. 13)

k
0   
1   
2   
3   
4   
5   
6   
7   
8   
9   
10   
100   
1000   
10000   
100000   
1000000   
10000000   
100000000   
 		     1,00000000000
    1,11111111111
    1,15111111111
    1,17151927438
    1,18386495339
    1,19212941620
    1,19804657596
    1,20249102041
    1,20595122802
    1,20872131112
    1,21098888482
    1,23122532283
    1,23345079991
    1,23367555264
    1,23369805016
    1,23370030014
    1,23370052514
    1,23370054563
    1,23370055014

Anhang 2

Gl. 4 ist ein Sonderfall der Riemannschen Zeta-Funktion.

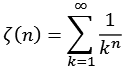      (Gl. 16)

Die Zeta Funktion läßt sich auch mit Hilfe der Bernoulli-Zahlen ausdrücken.

      (Gl. 17)

[zurück] [Inhaltsverzeichnis] [vor]