Aufgabe 41
|
[zurück] | Aufgabe 41 |
[vor] | |
Bei dieser Aufgabe geht es nicht darum eine Gleichung zu lösen sondern den Ausdruck ohne Benutzung eines Taschenrechners zu vereinfachen.
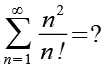(Gl. 1)
Für die Fakultät gilt.
(Gl. 2)
Gl. 2 setzen wir in Gl. 1 ein.
(Gl. 3)
Jetzt können wir einmal n kürzen.
(Gl. 4)
Den Zähler ergänzen wir mit -1+1.
(Gl. 5)
Den Bruch trennen wir in zwei Brüche.
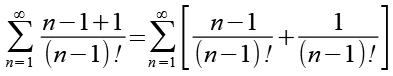(Gl. 6)
Die Summenfunktion teilen wir auf beide Brüche auf.
(Gl. 7)
Betrachten wir nur die erste Summenfunktion und separieren das erste Glied für n=1.
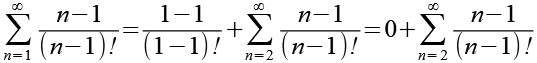(Gl. 8)
Das erste Glied ist Null und fällt weg.
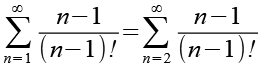(Gl. 9)
Gl. 9 setzen wir in Gl. 7 ein.
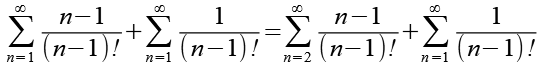(Gl. 10)
Für die Fakultät gilt.
(Gl. 11)
Gl. 11 setzen wir in Gl. 10 ein.
(Gl. 12)
Bei der ersten Summenfunktion können wir (n-1) kürzen.
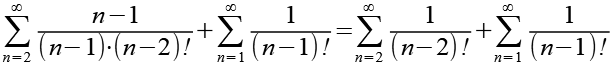(Gl. 13)
Wir berechnen die ersten Glieder der beiden Summenfunktionen.
(Gl. 14)
Betrachten wir die Reihenentwicklung der Exponentialfunktion.
(Gl. 15)
Für x=1 erhalten wir.
(Gl. 16)
Gl. 16 setzen wir in Gl. 14 ein.
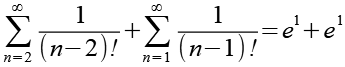(Gl. 17)
Als Ergebnis erhalten wir für Gl. 1.
(Gl. 18)
Anhang
Untersuchen wir die Konvergenz der Reihe.
| n | |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
1,00000000000 3,00000000000 4,50000000000 5,16666666667 5,37500000000 5,42500000000 5,43472222222 5,43630952381 5,43653273810 5,43656029541 5,43656332672 5,43656362734 5,43656365448 5,43656365673 5,43656365690 5,43656365692 |
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |