Aufgabe 40
|
[zurück] | Aufgabe 40 |
[vor] | |
Bei dieser Aufgabe geht es nicht darum eine Gleichung zu lösen sondern den Ausdruck ohne Benutzung eines Taschenrechners zu vereinfachen.
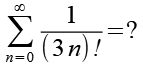(Gl. 1)
Die Reihenentwicklung.
(Gl. 2)
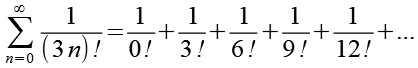(Gl. 3)
Es gilt.
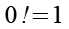(Gl. 4)
Mit Hilfe von Gl. 4 erhalten wir aus Gl. 3.
(Gl. 5)
Für die Reihenentwicklung der Exponentialfunktion gilt.
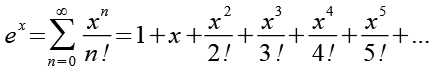(Gl. 6)
Für die weitere Berechnung benötigen wir die kubischen Einheitswurzeln (1, w, w2), siehe Anhang 2. Für die kubischen Einheitswurzeln gilt.
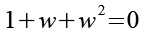(Gl. 7)
(Gl. 8)
Die kubischen Einheitswurzeln (1, w, w2) setzen wir in Gl. 6 ein.
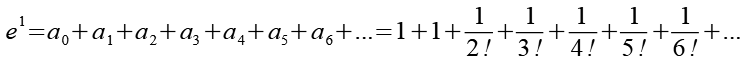(Gl. 9)
(Gl. 10)
(Gl. 11)
Jetzt addieren wir die einzelnen Glieder von Gl. 9, Gl. 10 und Gl. 11.
(Gl. 12)
Zur besseren Übersichtlichkeit habe ich die einzelnen Glieder mit a, b und c bezeichnet. Zur Vereinfachung wenden wir Gl. 7 und Gl. 8 an.
(Gl. 13)
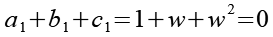(Gl. 14)
(Gl. 15)
(Gl. 16)
(Gl. 17)
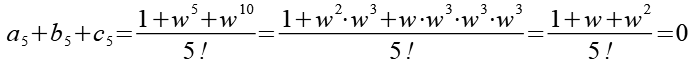(Gl. 18)
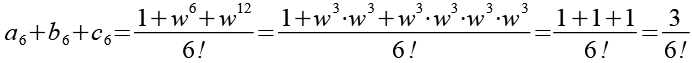(Gl. 19)
Für Gl. 12 erhalten wir.
(Gl. 20)
Einige Glieder sind Null.
(Gl. 21)
Die 3 können wir ausklammern.
(Gl. 22)
Beide Seiten teilen wir durch 3.
(Gl. 23)
Jetzt vergleichen wir Gl. 23 mit Gl. 5.
(Gl. 5)
Die rechten Seiten von Gl. 23 und Gl. 5 sind identisch, damit haben wir die Lösung.
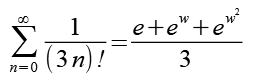(Gl. 24)
Anhang 1
Untersuchen wir die Konvergenz der Reihe.
| n | |
|
0 1 2 3 4 5 6 7 8 9 10 |
1,00000000000 1,16666666667 1,16805555556 1,16805831129 1,16805831338 1,16805831338 1,16805831338 1,16805831338 1,16805831338 1,16805831338 1,16805831338 |
Anhang 2
Die kubischen Einheitswurzeln (1, w, w2) sind die Lösung folgender Gleichung.
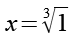(Gl. 25)
Die drei Lösungen x1, x2 und x3 der Gl. 25.
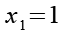(Gl. 26)
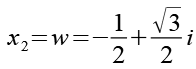(Gl. 27)
(Gl. 28)
x2 und x3 sind konjugiert komplexe Zahlen.
Für die Multiplikation komplexer Zahlen gilt.
(Gl. 29)
Für das Quadrat einer komplexem Zahl gilt.
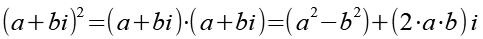(Gl. 30)
x2 bzw. w setzen wir in Gl. 30 ein, das Ergebnis ist x3 bzw. w2.
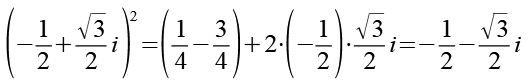(Gl. 31)
Es gilt.
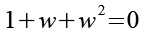(Gl. 7)
x1, x2 und x3 setzen wir in Gl. 7 ein, das Ergebnis ist Null.
(Gl. 32)
Für die 3. Potenz einer komplexen Zahl gilt.
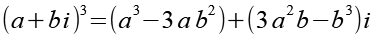(Gl. 33)
Zur Kontrolle setzen wir x2 bzw. w in Gl. 33 ein, das Ergebnis ist 1.
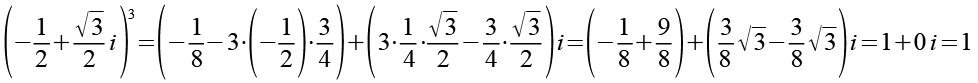(Gl. 34)
Zur Kontrolle setzen wir x3 bzw. w2 in Gl. 33 ein, das Ergebnis ist 1.
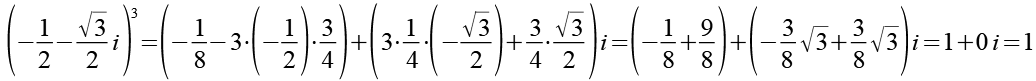(Gl. 35)
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |