| [zurück] | Aufgabe 38 |
[vor] |
Bei dieser Aufgabe geht es nicht darum eine Gleichung zu lösen sondern den Ausdruck ohne Benutzung eines Taschenrechners zu vereinfachen.
![]()
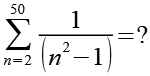 (Gl. 1)
(Gl. 1)
Die 1 im Nenner ersetzen wir durch 12.
![]()
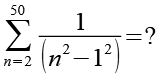 (Gl. 2)
(Gl. 2)
Es gilt.
![]()
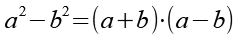 (Gl. 3)
(Gl. 3)
Mit Hilfe von Gl. 3 erhalten wir aus Gl. 2.
![]()
 (Gl. 4)
(Gl. 4)
Die 1 im Zähler ersetzen wir durch ein komplizierteres Konstrukt. Ziel ist es den Bruch so in zwei Teilbrüche zu teilen dass man auch Teile kürzen kann.
![]()
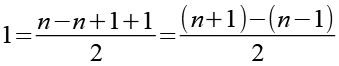 (Gl. 5)
(Gl. 5)
Wir setzen Gl. 5 in Gl. 4 ein.
![]()
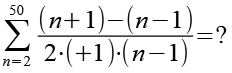 (Gl. 6)
(Gl. 6)
Den Faktor 2 im Nenner ziehen wir vor das Summenzeichen.
![]()
 (Gl. 7)
(Gl. 7)
Den Bruch teilen wir in zwei Teilbrüche.
![]()
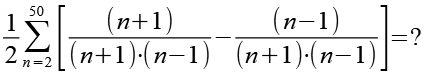 (Gl. 8)
(Gl. 8)
Wir können einmal (n+1) und einmal (n-1) kürzen.
![]()
 (Gl. 9)
(Gl. 9)
Wir teilen die Summenfunktion auf.
![]()
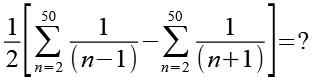 (Gl. 10)
(Gl. 10)
Die Glieder der ersten Summenfunktion.
![]()
 (Gl. 11)
(Gl. 11)
Die Glieder der zweiten Summenfunktion.
![]()
 (Gl. 12)
(Gl. 12)
Wir setzen Gl. 11 und Gl. 12 in Gl. 10 ein.
![]()
 (Gl. 13)
(Gl. 13)
Die einzelnen Glieder sortieren wir nach dem Nenner.
![]()
 (Gl. 14)
(Gl. 14)
Durch das Vorzeichen heben sich die Glieder in der Mitte auf, es bleiben nur die ersten beiden und die letzten beiden Glieder stehen.
![]()
 (Gl. 15)
(Gl. 15)
Jetzt müssen wir die Brüche nur noch auf einen Hauptnenner bringen.
![]()
 (Gl. 16)
(Gl. 16)
![]()
 (Gl. 17)
(Gl. 17)
Das Ergebnis.
![]()
 (Gl. 18)
(Gl. 18)
Anhang 1
Untersuchen wir die Konvergenz der Reihe.
| n | Summe |
|
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
0,333333333333 0,458333333333 0,525000000000 0,566666666667 0,595238095238 0,616071428571 0,631944444444 0,644444444444 0,654545454545 0,662878787879 0,669871794872 0,675824175824 0,680952380952 0,685416666667 0,689338235294 0,692810457516 0,695906432749 0,698684210526 0,701190476190 0,703463203463 0,705533596838 0,707427536232 0,709166666667 0,710769230769 0,712250712251 0,713624338624 0,714901477833 0,716091954023 0,717204301075 0,718245967742 0,719223484848 0,720142602496 0,721008403361 0,721825396825 0,722597597598 0,723328591750 0,724021592443 0,724679487179 0,725304878049 0,725900116144 0,726467331118 0,727008456660 0,727525252525 0,728019323671 0,728492136910 0,728945035461 0,729379251701 0,729795918367 0,730196078431 |
Anhang 2
Aus Gl. 4 und Gl. 9 ergibt sich eine optisch schöne Gleichung, die Korrektheit läßt sich leicht beweisen.
![]()
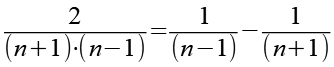 (Gl. 19)
(Gl. 19)
Beide Seiten multiplizieren wir mit (n+1).
![]()
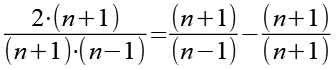 (Gl. 20)
(Gl. 20)
(n+1) können wir teilweise kürzen.
![]()
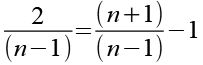 (Gl. 21)
(Gl. 21)
Die rechte Seite bringen wir auf den Nenner (n-1).
![]()
 (Gl. 22)
(Gl. 22)
Aus der rechten Seite machen wir einen Bruch.
![]()
 (Gl. 23)
(Gl. 23)
![]()
 (Gl. 24)
(Gl. 24)
Beide Seiten m ultilizieren wir mit (n-1).
![]()
 (Gl. 25)
(Gl. 25)
![]()
 (Gl. 26)
(Gl. 26)
Anhang 3
Die 48 Brüche kann man auch per Hand addieren. Das ist natürlich mathematisch trivial, man muss es aber ohne Fehler schaffen.
![]()

Um das Addieren der Brüche zu vereinfachen habe ich von den 48 Nennern die Primfaktorzerlegung berechnet.
| n | n2-1 | Primfaktorzerlegung |
|
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 |
3 8 15 24 35 48 63 80 99 120 143 168 195 224 255 288 323 360 399 440 483 528 575 624 675 728 783 840 899 960 1023 1088 1155 1224 1295 1368 1443 1520 1599 1680 1763 1848 1935 2024 2115 2208 2303 2400 2499 |
3 2·2·2 3·5 2·2·2·3 5·7 2·2·2·2·3 3·3·7 2·2·2·2·5 3·3·11 2·2·2·3·5 11·13 2·2·2·3·7 3·5·13 2·2·2·2·2·7 3·5·17 2·2·2·2·2·3·3 17·19 2·2·2·3·3·5 3·7·19 2·2·2·5·11 3·7·23 2·2·2·2·3·11 5·5·23 2·2·2·2·3·13 3·3·3·5·5 2·2·2·7·13 3·3·3·29 2·2·2·3·5·7 29·31 2·2·2·2·2·2·3·5 3·11·31 2·2·2·2·2·2·17 3·5·7·11 2·2·2·3·3·17 5·7·37 2·2·2·3·3·19 3·13·37 2·2·2·2·5·19 3·13·41 2·2·2·2·3·5·7 41·43 2·2·2·3·7·11 3·3·5·43 2·2·2·11·23 3·3·5·47 2·2·2·2·2·3·23 7·7·47 2·2·2·2·2·3·5·5 3·7·7·17 |
Die Brüche habe ich von a1 bis a48 nummeriert. Ich habe sie zuerst paarweise addiert, die Auswahl erfolgte nach Gefühl welche Brüche gut zusammenpassen.
![]()

![]()

![]()
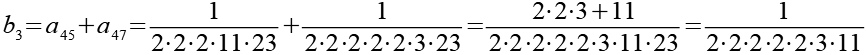
![]()

![]()
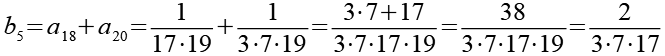
![]()

![]()

![]()
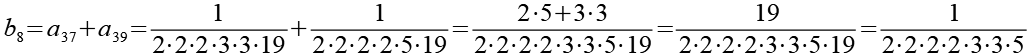
![]()

![]()
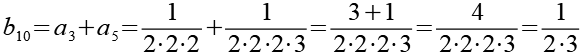
![]()
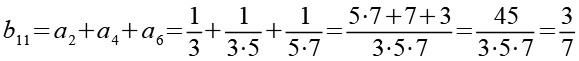
![]()
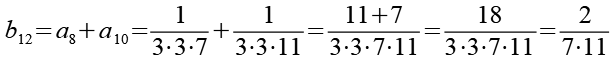
![]()

![]()

![]()

![]()

![]()
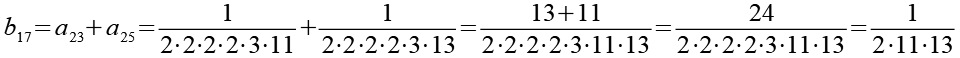
![]()
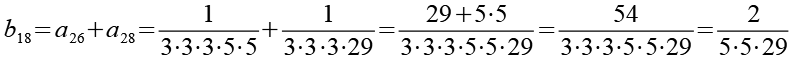
![]()
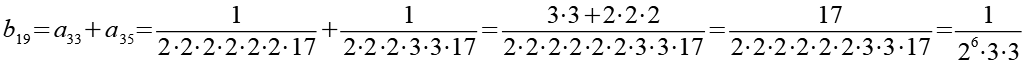
![]()

![]()

![]()
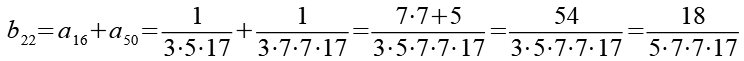
![]()

![]()
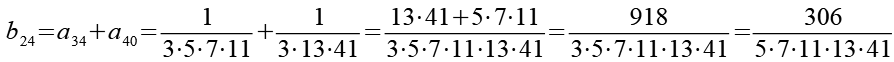
Im zweiten Schritt werden die 24 Brüche (b1 bis b24) wieder paarweise addiert.
![]()
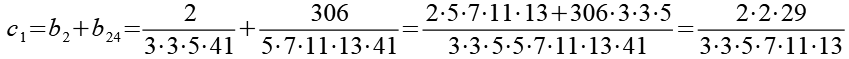
![]()

![]()

![]()
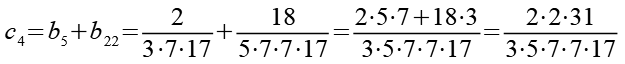
![]()
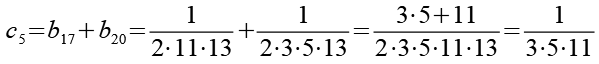
![]()
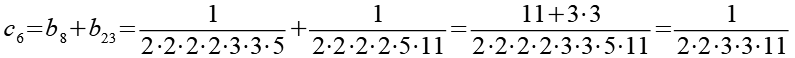
![]()
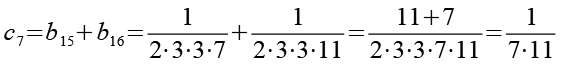
![]()

![]()

![]()

![]()
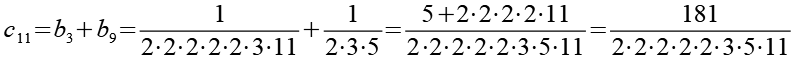
![]()

Im dritten Schritt werden die 12 Brüche (c1 bis c12) wieder paarweise addiert.
![]()

![]()
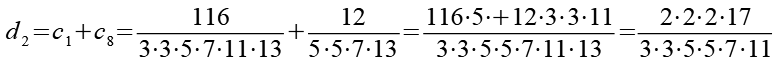
![]()
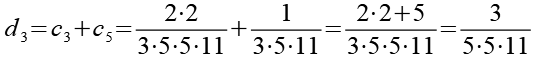
![]()

![]()
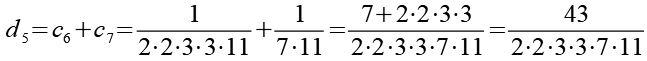
![]()

Im vierten Schritt werden die 6 Brüche (d1 bis d6) wieder paarweise addiert.
![]()

![]()

![]()
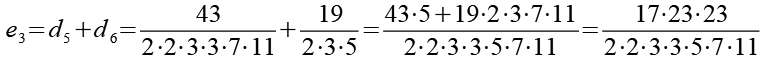
Im letzten Schritt werden e1, e2 und e3 addiert.
![]()
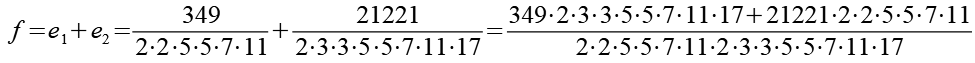
![]()

![]()
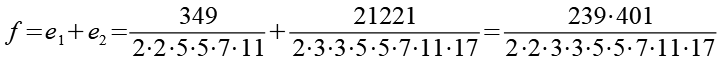
![]()

![]()
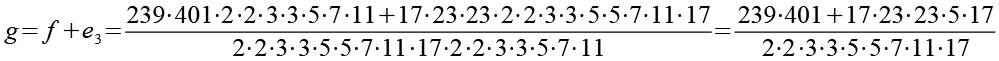
![]()

| [zurück] | [Inhaltsverzeichnis] | [vor] |