Interessante Mathe Aufgaben

Bei dieser Aufgabe geht es nicht darum eine Gleichung zu lösen sondern den Ausdruck ohne Benutzung eines Taschenrechners zu vereinfachen.

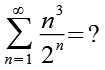(Gl. 1)

Wir stellen Gl. 1 ein bischen um.

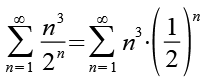(Gl. 2)

1/2 substituieren durch x.

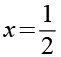(Gl. 3)

Gl. 3 setzen wir in Gl. 2 ein.

(Gl. 4)

Für eine geometrische Reihe mit |x|<1 gilt. Für diese Reihe ist auch der Grenzwert definiert.

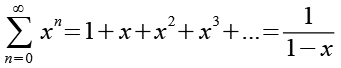(Gl. 5)

Diese Reihe hat schon große Ähnlichkeit mit Gl. 4. Es fehlt allerdings die Laufvariable n vor dem x, dies können wir aber erreichen wenn wir Gl. 5 differenzieren. Für die Ableitung der Potenzfunktion xⁿ siehe Anhang 1.

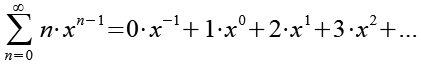(Gl. 6)

Das erste Glied dieser Reihe ist immer Null, wir können daher den Startwert entsprechend anpassen.

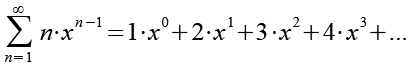(Gl. 7)

Jetzt müssen wir noch die rechte Seite differenzieren, siehe Anhang 2. Wir erhalten Gl. 8.

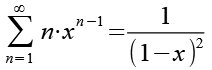(Gl. 8)

Um xⁿ wieder herzustellen multiplizieren wir beide Seiten mit x.

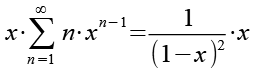(Gl. 9)

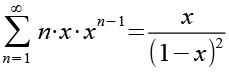(Gl. 10)

Mit Gl. 11 kommen wir Gl. 4 schon näher, den Vorgang des Differenzierens mit anschließender Multiplikation mit x müssen wir noch zweimal wiederholen.

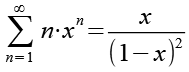(Gl. 11)

Beide Seiten werden differenziert, zur rechten Seite siehe Anhang 3.

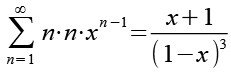(Gl. 12)

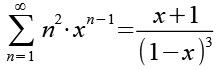(Gl. 13)

Beide Seiten werden mit x multipliziert.

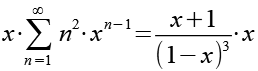(Gl. 14)

(Gl. 15)

Beide Seiten werden differenziert, zur rechten Seite siehe Anhang 4.

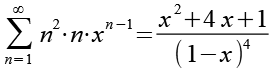(Gl. 16)

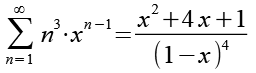(Gl. 17)

Beide Seiten werden mit x multipliziert.

(Gl. 18)

(Gl. 19)

Jetzt müssen wir nur noch Gl. 3 in Gl. 19 einsetzen.

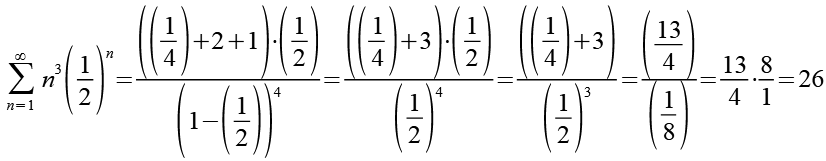(Gl. 20)

Das Ergebnis

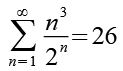(Gl. 21)

Anhang 1

Für die Ableitung der Potenzfunktion gilt.

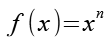(Gl. 22)

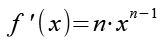(Gl. 23)

Anhang 2

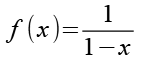(Gl. 24)

Für die Ableitung nutzen wir die Quotientenregel.

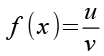(Gl. 25)

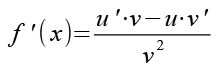(Gl. 26)

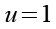(Gl. 27)

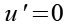(Gl. 28)

(Gl. 29)

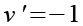(Gl. 30)

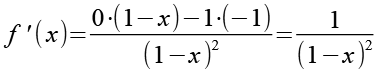(Gl. 31)

Anhang 3

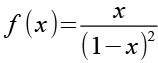(Gl. 32)

Für die Ableitung nutzen wir die Quotientenregel.

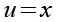(Gl. 33)

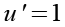(Gl. 34)

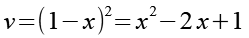(Gl. 35)

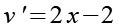(Gl. 36)

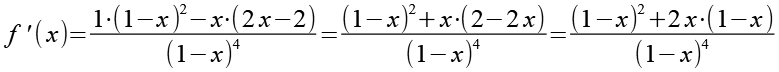(Gl. 37)

(Gl. 38)

(Gl. 39)

Anhang 4

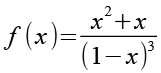(Gl. 40)

Für die Ableitung nutzen wir die Quotientenregel.

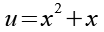(Gl. 41)

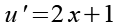(Gl. 42)

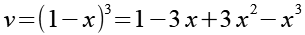(Gl. 43)

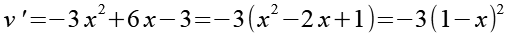(Gl. 44)

(Gl. 45)

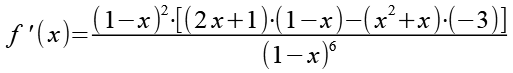(Gl. 46)

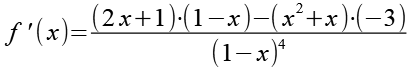(Gl. 47)

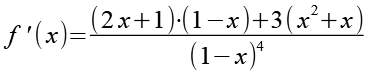(Gl. 48)

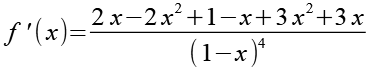(Gl. 49)

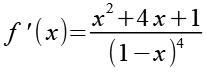(Gl. 50)

Anhang 5

Untersuchen wir die Konvergenz der Reihe.

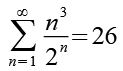(Gl. 21)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52

    0,50000000000
    2,50000000000
    5,87500000000
    9,87500000000
    13,7812500000
    17,1562500000
    19,8359375000
    21,8359375000
    23,2597656250
    24,2363281250
    24,8862304688
    25,3081054688
    25,5762939453
    25,7437744141
    25,8467712402
    25,9092712402
    25,9467544556
    25,9690017700
    25,9820842743
    25,9897136688
    25,9941296577
    25,9966683388
    25,9981187582
    25,9989427328
    25,9994083941
    25,9996702969
    25,9998169467
    25,9998987243
    25,9999441523
    25,9999692980
    25,9999831705
    25,9999907999
    25,9999949835
    25,9999972713
    25,9999985192
    25,9999991981
    25,9999995667
    25,9999997663
    25,9999998742
    25,9999999324
    25,9999999637
    25,9999999806
    25,9999999896
    25,9999999945
    25,9999999970
    25,9999999984
    25,9999999992
    25,9999999996
    25,9999999998
    25,9999999999
    25,9999999999
    26,0000000000

Anhang 6

Ein paar Variationen von Gl. 1

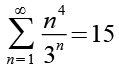(Gl. 51)

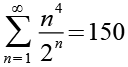(Gl. 52)

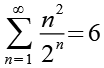(Gl. 53)

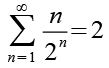(Gl. 54)

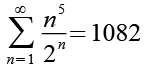(Gl. 55)

[zurück]

[Inhaltsverzeichnis]

[vor]