[zurück]

Interessante Mathe Aufgaben

 [vor]

Bei dieser Aufgabe geht es nicht darum eine Gleichung zu lösen sondern den Ausdruck ohne Benutzung eines Taschenrechners zu vereinfachen.

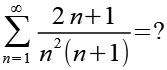      (Gl. 1)

Im Zähler des Bruches ersetzen wir die 2n durch n+n.

      (Gl. 2)

Den Bruch teilen wir in zwei Brüche.

      (Gl. 3)

Im ersten Bruch können wir n, im zweiten Bruch können wir n+1 kürzen.

      (Gl. 4)

Betrachten wir den ersten Bruch. Zum Zähler addieren wir n-n ohne den Wert zu verändern. Dadurch können wir den Bruch in zwei Brüche teilen.

      (Gl. 5)

Das Ergebnis von Gl. 5 setzen wir in Gl. 4 ein.

      (Gl. 6)

Die Summe teilen wir in zwei Summen auf.

      (Gl. 7)

Betrachten wir zuerst die erste Summe und schauen uns die Glieder der Folge an.

      (Gl. 8)

Bis auf das erste Glied besteht die Folge aus Brüchen die sich wegen des unterschiedlichen Vorzeichens aufheben, Das Ergebnis der Folge ist 1.

      (Gl. 9)

Das Ergebnis dieser Folge entnehmen wir der Literatur (siehe Leonhard Eulert).

      (Gl. 10)

      (Gl. 11)

Das Ergebnis von Gl. 8 und Gl. 10 setzen wir in Gl. 7 ein.

      (Gl. 12)

Als Ergebnis erhalten wir.

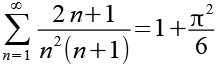      (Gl. 13)

Anhang 1

Untersuchen wir die Konvergenz der Reihe.

      (Gl. 14)

k x
1   
2   
3   
4   
5   
6   
7   
8   
9   
10   
100   
1000   
10000   
100000   
1000000   
10000000   
100000000   		     0,500000000000
    0,666666666667
    0,750000000000
    0,800000000000
    0,833333333333
    0,857142857143
    0,875000000000
    0,888888888889
    0,900000000000
    0,909090909091
    0,990099009901
    0,999000999001
    0,999900009999
    0,999990000100
    0,999999000001
    0,999999900000
    0,999999989827
    1,000000000000

Anhang 2

Untersuchen wir die Konvergenz der Reihe.

      (Gl. 15)

k x
1   
2   
3   
4   
5   
6   
7   
8   
9   
10   
100   
1000   
10000   
100000   
1000000   
10000000   
100000000   
 		     1,00000000000
    1,25000000000
    1,36111111111
    1,42361111111
    1,46361111111
    1,49138888889
    1,51179705215
    1,52742205215
    1,53976773117
    1,54976773117
    1,63498390018
    1,64393456668
    1,64483407185
    1,64492406690
    1,64493306685
    1,64493396685
    1,64493405783
    1,64493406685

Anhang 3

Untersuchen wir die Konvergenz der Reihe.

      (Gl. 16)

k x
1   
2   
3   
4   
5   
6   
7   
8   
9   
10   
100   
1000   
10000   
100000   
1000000   
10000000   
100000000   
 		     1,50000000000
    1,91666666667
    2,11111111111
    2,22361111111
    2,29694444444
    2,34853174603
    2,38679705215
    2,41631094104
    2,43976773117
    2,45885864026
    2,62508291009
    2,64293556568
    2,64473408185
    2,64491406700
    2,64493206685
    2,64493386685
    2,64493404882
    2,64493406685

[zurück] [Inhaltsverzeichnis] [vor]