Interessante Mathe Aufgaben
|
[zurück] | Interessante Mathe Aufgaben |
[vor] | |
Bei dieser Aufgabe geht es nicht darum eine Gleichung zu lösen sondern den Ausdruck ohne Benutzung eines Taschenrechners zu vereinfachen.
Es gilt.
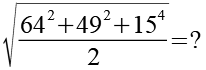(Gl. 1)
Die 64 ersetzen wir durch 82 und die 49 durch 72, die 15 ersetzen wir durch 8+7.
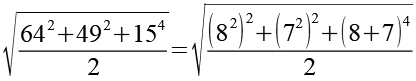(Gl. 2)
Es gilt.
(Gl. 3)
Mit Hilfe von Gl. 3 erhalten wir.
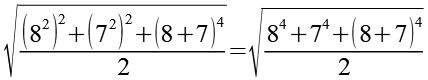(Gl. 4)
Die 8 substituieren wir durch x und die 7 durch y.
(Gl. 5)
(Gl. 6)
Gl. 5 und Gl. 6 setzen wir in Gl. 4 ein.
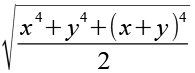(Gl. 7)
Es gilt.
(Gl. 8)
Gl. 8 setzen wir in Gl. 7 ein.
(Gl. 9)
(Gl. 10)
(Gl. 11)
Die 2 können wir kürzen.
(Gl. 12)
Die 3x2y2 ersetzen wir durch 2x2y2+x2y2.
(Gl. 13)
2 xy können wir ausklammern.
(Gl. 14)
Es gilt.
(Gl. 15)
Mit a=x2 und b=y2 erhalten wir aus Gl. 15.
(Gl. 16)
Gl. 16 setzen wir in Gl. 14 ein.
(Gl. 17)
Die x2y2 ersetzten wir durch (xy)2.
(Gl. 18)
Jetzt substituieren wir x2+y2 durch a und xy durch b.
(Gl. 19)
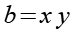(Gl. 20)
Gl. 19 und Gl. 20 setzen wir in Gl. 18 ein.
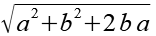(Gl. 21)
Es gilt.
(Gl. 22)
Mit Hilfe von Gl. 22 erhalten wir aus Gl. 21. Wurzel und Quadrat heben sich auf.
(Gl. 23)
Jetzt setzen wir Gl. 19 und Gl. 20 in Gl. 23 ein.
(Gl. 24)
x und y ersetzen wir durch 8 und 7 und erhalten 169.
(Gl. 25)
Die Lösung von Gl. 1.
(Gl. 26)
Anhang
Mit Hilfe der Candido's Identität läßt sich die Berechnung vereinfachen.
Es gilt.
(Gl. 27)
Gl. 27 wenden wir auf Gl. 4 an.
(Gl. 28)
(Gl. 29)
(Gl. 30)
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |