[zurück]

Interessante Mathe Aufgaben

[vor]

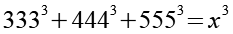      (Gl. 1)

Es gilt.

      (Gl. 2)

Mit Hilfe von Gl. 2 erhalten wir.

      (Gl. 3)

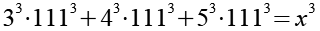      (Gl. 4)

111³ können wir ausklammern.

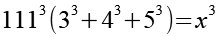      (Gl. 5)

      (Gl. 6)

      (Gl. 7)

Beide Seiten potenzieren wir mit 1/3.

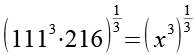      (Gl. 8)

Mit Hilfe von Gl. 2 erhalten wir.

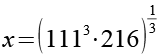      (Gl. 9)

      (Gl. 10)

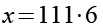      (Gl. 11)

      (Gl. 12)

Kontrolle

Zur Kontrolle setzen wir Gl. 12 in Gl. 1 ein.

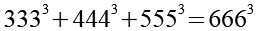      (Gl. 12a)

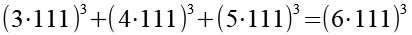      (Gl. 13)

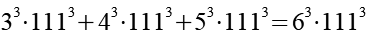      (Gl. 14)

      (Gl. 15)

      (Gl. 16)

      (Gl. 17)

Gl. 12a können wir auch allgemein schreiben mit n = 111.

      (Gl. 18)

Anhang

Die Richtigkeit von Gl. 15 läßt sich leicht beweisen.

      (Gl. 15)

Die 4 ersetzen wir durch 3+1, die 5 durch 3+2 und die 6 durch 3+3.

      (Gl. 19)

Die 3 ersetzen wir durch a.

      (Gl. 20)

Es gilt.

      (Gl. 21)

Mit Hilfe von Gl. 21 erhalten wir.

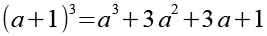      (Gl. 22)

      (Gl. 23)

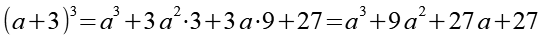      (Gl. 24)

Gl. 22, Gl. 23 und Gl. 24 setzen wir in Gl. 20 ein.

      (Gl. 25)

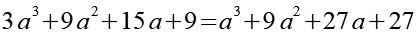      (Gl. 26)

Auf beiden Seiten subtrahieren wir 9a².

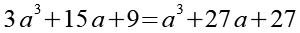      (Gl. 27)

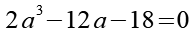      (Gl. 28)

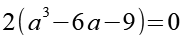      (Gl. 29)

Wir erhalten eine kubische Gleichung.

      (Gl. 30)

Für die Lösung dieser kubischen Gleichung dient die Cardanische Formel.

      (Gl. 31)

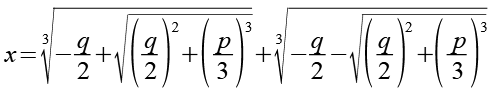      (Gl. 32)

Mit p=-6 und q=-9 erhalten wir.

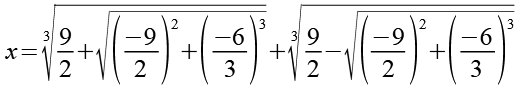      (Gl. 33)

      (Gl. 34)

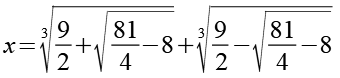      (Gl. 35)

      (Gl. 36)

      (Gl. 37)

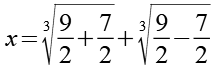      (Gl. 38)

      (Gl. 39)

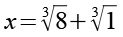      (Gl. 40)

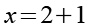      (Gl. 41)

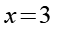      (Gl. 42)

Mit x bzw. a=3 haben wir Gl. 15 bewiesen.

[zurück]

[Inhaltsverzeichnis]

[vor]