Interessante Mathe Aufgaben
|
[zurück] | Interessante Mathe Aufgaben |
[vor] | |
(Gl. 1)
Die Fakultät n! ist wie folgt definiert.
(Gl. 2)
Die Fakltät kann auch rekursiv dargestellt werden.
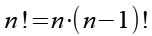(Gl. 3)
Mit Hilfe von Gl. 3 können wir Gl. 1 anders darstellen.
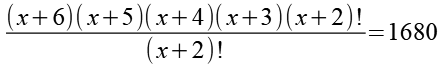(Gl. 4)
In Gl. 4 können wir (x + 2)! kürzen.
(Gl. 5)
Wir ändern die Reihenfolge der Klammern.
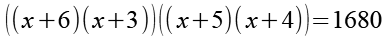(Gl. 6)
Die Klammern werden paarweise ausmultipliziert.
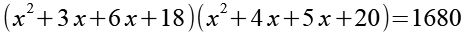(Gl. 7)
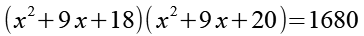(Gl. 8)
In Gl. 8 ersetzen wir die 18 durch 19-1 und die 20 durch 19+1.
(Gl. 9)
Wir substituieren x2 + 9x + 19 durch u.
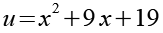(Gl. 10)
Wir setzen Gl. 10 in Gl. 9 ein.
(Gl. 11)
Es gilt:
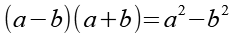(Gl. 12)
Mit Hilfe von Gl. 12 erhalten wir aus Gl. 11.
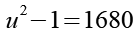(Gl. 13)
Auf beiden Seiten addieren wir 1.
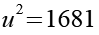(Gl. 14)
Auf beiden Seiten ziehen wir die Wurzel.
(Gl. 15)
Für u erhalten wir.
(Gl. 16)
Gl. 16 setzen wir in Gl. 10 ein.
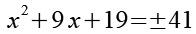(Gl. 17)
Fangen wir mit +41 an.
(Gl. 18)
Auf beiden Seiten subtrahieren wir 41.
(Gl. 19)
Wir erhalten folgende quadratische Gleichung.
(Gl. 20)
Für die Lösung der quadratischen Gleichung gilt.
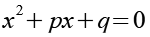(Gl. 21)
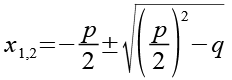(Gl. 22)
Für die Lösung von Gl. 20 erhalten wir.
(Gl. 23)
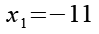(Gl. 24)
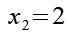(Gl. 25)
Die zweite Variante von Gl. 17.
(Gl. 26)
Auf beiden Seiten addieren wir 41.
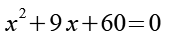(Gl. 27)
Für die Lösung von Gl. 27 erhalten wir.
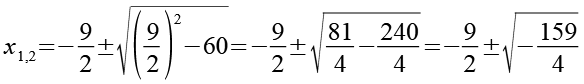(Gl. 28)
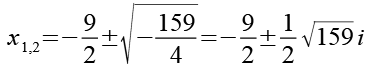(Gl. 29)
Die Lösung von Gl. 27 sind zwei konjugiert komplexe Zahlen.
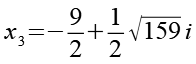(Gl. 30)
(Gl. 31)
Für Gl. 5 gibt es 4 Lösungen.
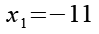
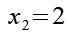
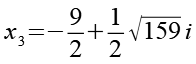
Kontrolle
Von den 4 Lösungen ist nur x2 = 2 eine Lösung für Gl. 1. Wir setzen x2 = 2 in Gl. 1 ein.
(Gl. 32)
Aus Gl. 32 erhalten wir.
(Gl. 33)
Analog zu Gl. 4 erhalten wir.
(Gl. 34)
Wir können 4! kürzen.
(Gl. 35)
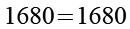(Gl. 36)
Wir setzen auch x1 = -11 in Gl. 5 ein, für Gl. 1 ist es natürlich keine Lösung.
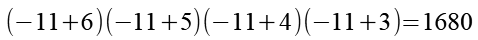(Gl. 37)
(Gl. 38)
(Gl. 39)
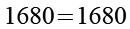(Gl. 36)
Der Vollständigkeit halber setzen wir auch dir beiden komplexen Löungen x3 und x4 in Gl. 5 ein, fangen wir mir x3 an.
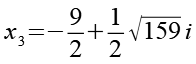(Gl. 30)
(Gl. 40)
Für die Multiplikation komplexer Zahlen gilt.
(Gl. 41)
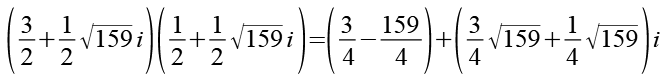(Gl. 42)
(Gl. 43)
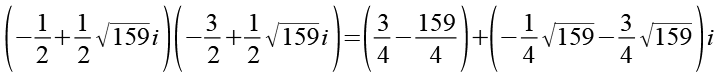(Gl. 44)
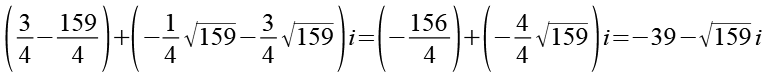(Gl. 45)
Zum Schluß multiplizieren wir das Ergebnis aus Gl. 43 und Gl. 45 und erhalten 1680.
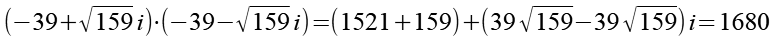(Gl. 46)
Die gleiche Rechnung für x4.
(Gl. 31)
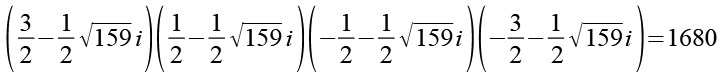(Gl. 47)
(Gl. 48)
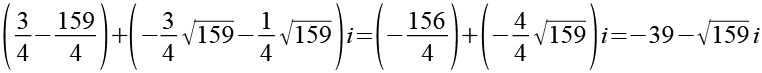(Gl. 49)
(Gl. 50)
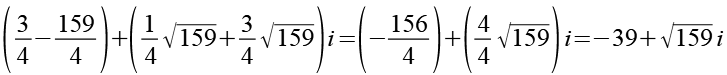(Gl. 51)
Zum Schluß multiplizieren wir das Ergebnis aus Gl. 49 und Gl. 51 und erhalten wieder 1680.
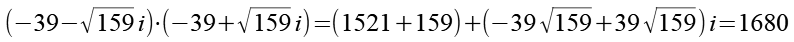(Gl. 52)
Anhang 1
Ein ganz anderer Lösungsansatz, bilden wir von 1680 die Primfaktorzerlegung.
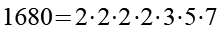(Gl. 53)
2*3=6 und 2*2*2=8.
(Gl. 54)
Wir setzen Gl. 54 in Gl. 5 ein.
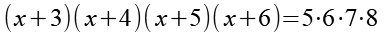(Gl. 55)
Aus Gl. 55 ist offensichtlich dass die Lösung x = 2 sein muss.
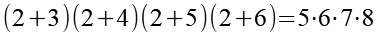(Gl. 56)
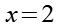(Gl. 57)
Anhang 2
Zum Vergleich verzichten wir auf die Umstellung von Gl. 5 (Gl. 6) und machen direkt mit Gl. 5 weiter.
(Gl. 58)
Wir multiplizieren die Klammern aus.
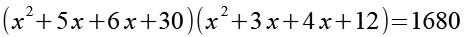(Gl. 59)
Wir erhalten einmal 11 x und einmal 7 x, es gibt jetzt keine Möglichkeit wie bei Gl. 8 etwas auszuklammern.
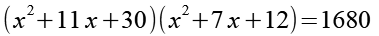(Gl. 60)
Wir multiplizieren die Klammern aus.
(Gl. 61)
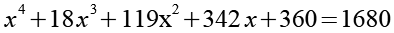(Gl. 62)
Wir erhalten ein Polynom 4. Grades.
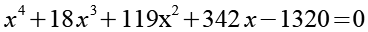(Gl. 63)
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |