| [zurück] | 3.78. Feder I |
[vor] |
Die Feder I [8] wird durch folgende Gleichungen dargestellt.
|
x = (R + r cos(v)) cos(u) |
3-253 |
|
|
y = (R + r cos(v)) sin(u) |
3-254 |
|
|
z = r (sin(v) + L u/pi) |
3-255 |
Die Konstanten R und r bestimmen die Radien der Feder, die Konstante L bestimmt die Steigung der Feder und die Konstante n die Anzahl der Windungen.
Die Gleichungen 3-253 und 3-254 entspechen exakt den Gleichungen für den Torus (3-181/182). Bei der Feder haben wir nur in Gl. 3-255 den Ausdruck L u/pi als lineare Steigung eingefügt.
Die einzelnen Kreissegmente sind bei dieser Feder alle parallel zur Achse z ausgerichtet. Das ist bei der Feder II anders.
Zur Darstellung der Fläche können die beiden Parameter u und v zum Beispiel folgende Werte (Definitionsbereich) annehmen.
|
u ist Element aus der Zahlenmenge [0, n 2 pi] |
||
|
v ist Element aus der Zahlenmenge [0, 2 pi] |
Bei der Feder-I handelt es sich um eine halboffene Figur, der Definitionsbereich von u kann daher beim Plugin verändert werden.
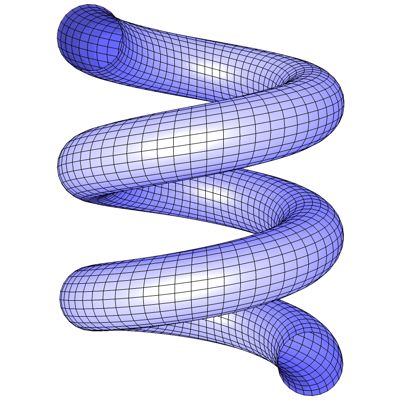
Abb. 82
Die Figur kann auf der nächsten Seite mit einem Java-Applet von allen Seiten betrachtet und gedreht werden.
| [zurück] | [Inhaltsverzeichnis] | [vor] |