Parametrische Flächen und Körper

3.223. Gyroid

Den Gyroid habe ich hier [38] gefunden, siehe auch Kapitel 6.1. Encyclopedia of Analytical Surfaces.

Der Gyroid wird durch folgende implizite Gleichung dargestellt.

223-1

Leider habe ich dazu keine parametrische Darstellung finden können, Gl. 1 läßt sich aber nach z auflösen.

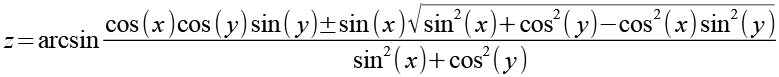223-2

Bei der Programmierung gibt es aber mehrere Probleme. Gl. 2 enthält eine Wurzel, dabei müssen negative Argumente berücksichtigt werden. Der arcsin ist auch nur zwischen -1 und 1 definiert. Mein Programm erzeugt aber eine exakt definierte Anzahl Punkte die nach festem Schema zu Polygonen verbunden werden. Punkte, die nicht definiert sind (z.B. negatives Argument der Wurzel), habe ich durch einen festen y-Wert ersetzt.

Abb. 223-1

Diese Punkte lassen sich in Cinema 4D leicht löschen.

Abb. 223-2

Abb. 3 zeigt beide Teile der Figur, blau für die positive Wurzel und rot für die negative Wurzel.

Abb. 223-3

Bei dieser geringen Auflösung (2500 Punkte) entstehen leider unschön ausgefranzte Ränder. Ich habe die Auflösung daher auf 25000000 Punkte erhöht.

Abb. 223-4

Abb. 223-5

xy
Abb. 223-6

xz
Abb. 223-7

yz
Abb. 223-8

Ich habe versucht ein Ergebnis von Gl. 2 wieder in Gl. 1 einzusetzen. Leider hat das nicht funktioniert, das Vorzeichen ist falsch. Vielleicht ist Gl. 2 aus [38] fehlerhaft, der Gyroid sieht aber nicht schlecht aus.

   x = -0,440
   y = 0,126
   z₁ = -0,300
   z₂ = 0,511

Mit z = +0,300 wird Gl. 1 erfüllt. Ich habe dann selbst versucht Gl. 1 nach z aufzulösen. Z kommt dabei sowohl als sin z und als cos z vor. Wir müssen daher cos z durch sin z ausdrücken.

223-3

Wir bringen cos z auf die rechte Seite.

223-4

Dann benötigen wir eine passende Formelsammlung [49].

223-5

Gl. wird nach cos x aufgelöst.

223-6

223-7

Gl. 7 setzen wir sinngemäß (mit z statt x) in Gl. 4 ein.

223-8

Beide Seiten werden quadriert und ausmultipliziert.

223-9

223-10

223-11

223-12

223-13

Nach ein bischen Umstellen erhalten wir eine quadratische Gleichung.

223-14

Zur Lösung der quadratische Gleichung benötigen wir wieder eine passende Formelsammlung [49].

223-15

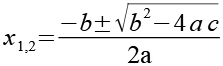223-16

Für die Koeffizienten der quadratische Gleichung erhalten wir.

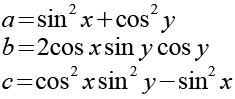223-19

Für sin z erhalten wir.

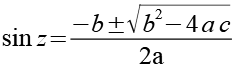223-17

Für z erhalten wir.

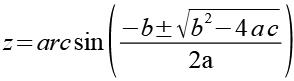223-18

Der Ausdruck unter der Wurzel läßt sich weiter vereinfachen, das machen wir aber Schrittweise.

223-20

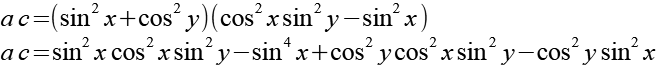223-21

223-22

223-23

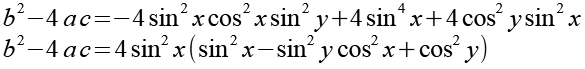223-24

Für z erhalten wir dann.

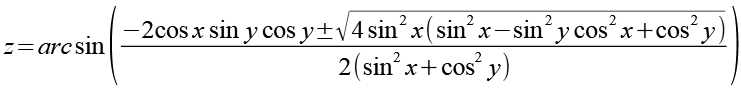223-25

Der Faktor 2 läßt sich noch eliminieren.

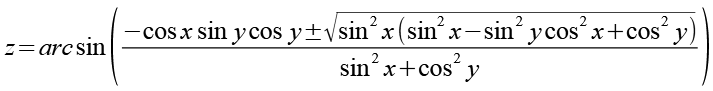223-26

Im Prinzip könnte man noch sin²x aus der Wurzel entfernen, das führt dann aber zu einem Rechenfehler. So führt Gl. 26 zum richtigen Ergebnis.

   x = -0,440
   y = 0,126
   z₁ = 0,300
   z₂ = -0,511

Gl. 3 (bzw. Gl. 1) wird mit z = 0,300 erfüllt.

Um den Gyroid korrekt darstellen zu können muss man einen anderen Weg gehen und sich nur aug Gl. 1 beschränken. Ich habe dazu ein Skript geschrieben das den Gyroid aus kleinen Würfeln zusammensetzt, das ergibt auch einen netten "Lego" Effekt.

[-pi pi, -pi pi,-pi pi]
Abb. 223-9