[zurück]

3.212. Balls Cylindroid

[vor]

Den Balls Cylindroid habe ich hier [38] gefunden, siehe auch Kapitel 6.1. Encyclopedia of Analytical Surfaces.

Der Balls Cylindroid wird durch folgende Gleichungen dargestellt.

212-1 212-2 212-3

Die implizite Darstellung lautet.

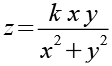212-4

Für die beiden Parameter u und v gilt folgender Definitionsbereich.

Für k = 2 erhält man den Plücker´s Conoid II, das läßt sich leicht beweisen. Dazu müssen wir Gl. 3 umformen.

212-5

Jetzt bemühen wir wieder eine gute Formelsammlung [49].

212-6

Jetzt setzen wir Gl. 6 in Gl. 5 ein und erhalten Gl. 192-3.

192-3

k = 1
Abb. 212-1

k = 2
Abb. 212-2

k = 3
Abb. 212-3

k = 5
Abb. 212-4

Zum Schluß möchte ich überprüfen ob die parametrische Darstellung auch der impliziten Darstellung entspricht.
Dazu setzen wir Gl. 1 und Gl. 2 in Gl. 4 ein.

212-5

Um Gl. 5 weiter zu vereinfachen benötigen wir eine passende Formelsammlung [49].

212-6

Gl. 6 setzen wir in Gl. 5 ein.

212-3

Wir erhalten wieder Gl. 3, was zu beweisen war.

[zurück]

[Inhaltsverzeichnis]

[vor]