[zurück]

3.190. Neovius Surface

 [vor]

Die Neovius Surface habe ich hier [38, 41] gefunden, siehe auch Kapitel 6.1. Encyclopedia of Analytical Surfaces.

Die Neovius Surface wird durch folgende Gleichungen dargestellt.

  190-1

190-2

190-3

Die implizite Darstellung lautet.

  190-4

Für die beiden Parameter u und v gilt folgender Definitionsbereich.

  u ist Element aus der Zahlenmenge [-pi/2, pi/2]
  v ist Element aus der Zahlenmenge [-pi/2, pi/2]


Abb. 190-1


Abb. 190-2
xy


Abb. 190-3
xz


Abb. 190-4
yz

Aus 8 Flächen kann man einen Würfel zusammenbauen.


Abb. 190-5

Zum Schluß möchte ich überprüfen ob die parametrische Darstellung auch der impliziten Darstellung entspricht. Mathematisch ist das trivial, das Problem ist eigentlich nur keine Schreib- oder Flüchtigkeitsfehler zu machen.
Zuerst multiplizieren wir die Klammer in Gl. 4 aus.

  190-5

Jetzt setzen wir Gl. 1, Gl. 2 und Gl. 3 in Gl. 5 ein.

 

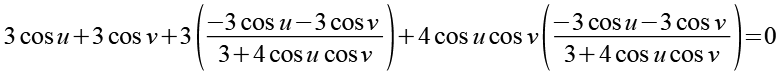190-6
 

190-7

Jetzt multiplizieren wir beide Seiten von Gl. 7 mit (3 + 4 cos u cos v).

  190-8

Nach dem ausmultiplizieren der Klammern läßt sich die Gleichung weiter vereinfachen.

 

Beide Seiten sind Null, was zu beweisen war.

Zum Schluß habe ich die Neovius Surface nach Gl. 4 aus kleinen Würfeln zusammengesetzt, dafür wurden 64 Millionen Punkte berechnet.


Abb. 190-6


Abb. 190-7

Abb. 7 aufgeschnitten.


Abb. 190-8

[zurück] [Inhaltsverzeichnis] [vor]