[zurück]

3.189. Cayley Surface

 [vor]

Die Cayley Surface habe ich hier [38] gefunden, siehe auch Kapitel 6.1. Encyclopedia of Analytical Surfaces.

Die Cayley Surface wird durch folgende Gleichungen dargestellt.

 
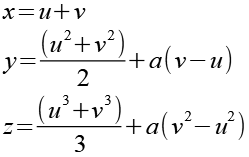189-1


189-2


189-3

Die implizite Darstellung lautet.

 
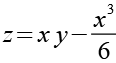189-4

Für die beiden Parameter u und v gilt folgender Definitionsbereich.

  u ist Element aus der Zahlenmenge [-1.5, 1.0]
  v ist Element aus der Zahlenmenge [-1.5, 1.5]


Abb. 189-1
a = 1


Abb. 189-2
xy


Abb. 189-3
xz


Abb. 189-4
yz

Zum Schluß möchte ich überprüfen ob die parametrische Darstellung auch der impliziten Darstellung entspricht. Mathematisch ist das trivial, das Problem ist eigentlich nur keine Schreib- oder Flüchtigkeitsfehler zu machen. Dazu setzen wir Gl. 1 und Gl. 2 in Gl. 4 ein. Um das etwas übersichtlicher zu gestalten gehen wir schrittweiser vor.
Fangen wir mit x3 an.

 





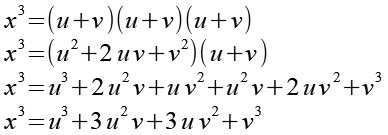189-5

Gl. 5 passen wir an Gl. 4 an.

 
189-6

Im nächsten Schritt berechnen wir x * y

 
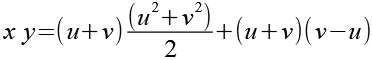189-7

Diese Berechnung teilen wir auch auf.

 

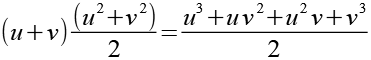189-8
 

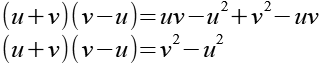189-9

Gl. 8 und Gl. 9 setzen wir in Gl. 7 ein.

 

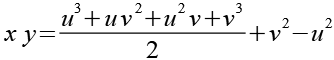189-10

In Gl. 10 bringen wir den Bruch auf den Nenner 6.

 

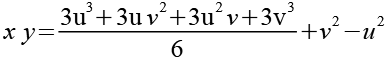189-11

Jetzt können wir Gl. 11 und Gl. 6 in Gl. 4 einsetzen und die Gleichung weiter vereinfachen.

 

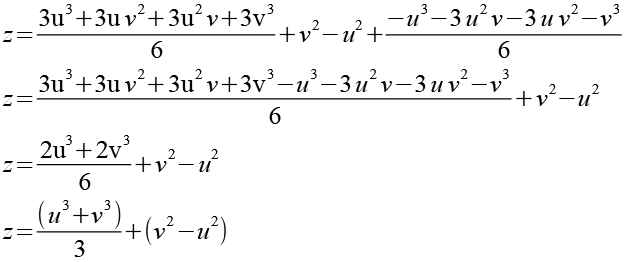Und wir erhalten wieder die implizite Darstellung Gl. 4, was zu beweisen war.

[zurück] [Inhaltsverzeichnis] [vor]