10.8. 6 5-Eck Prismen und 6 3-Eck Prismen
|
[zurück] | 10.8. 6 5-Eck Prismen und 6 3-Eck Prismen |
[vor] | |
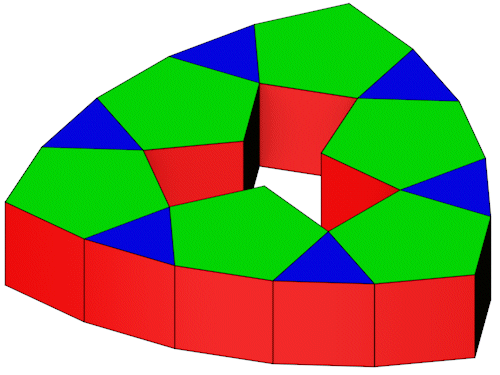
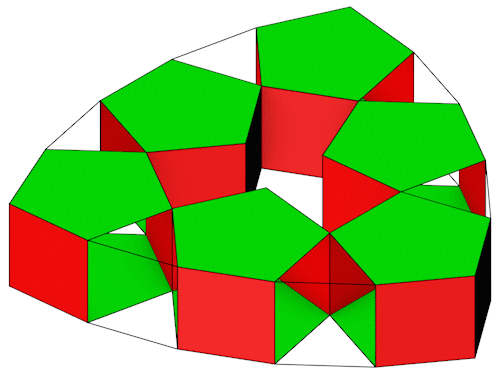
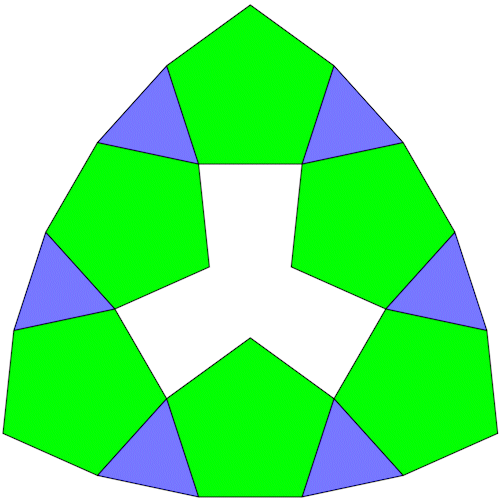
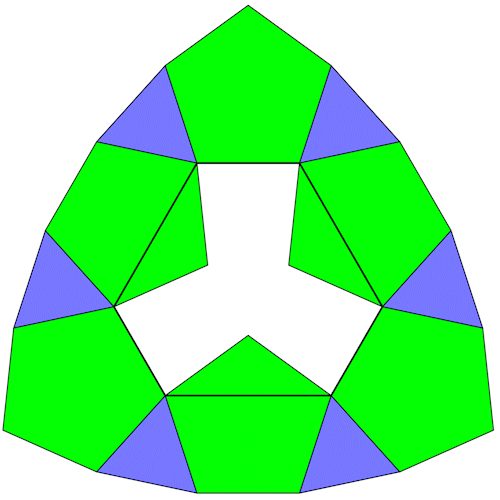
6 5-Eck Prismen lassen sich so anordnen das sie durch 6 3-Eck Prismen zu einem Ring verbunden werden können.
 |
 |
 |
 |
| Anzahl Ecken | 48 |
| Anzahl Flächen | 12 Dreiecke 24 Vierecke 12 Fünfecke |
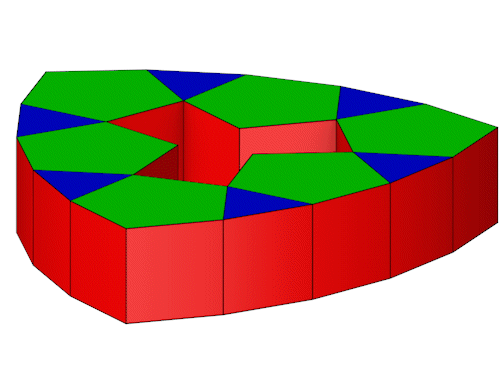
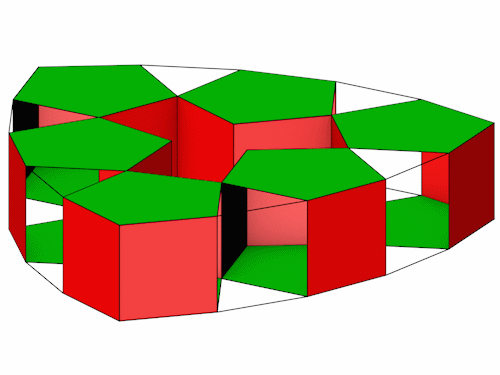
Die Seitenansichten.
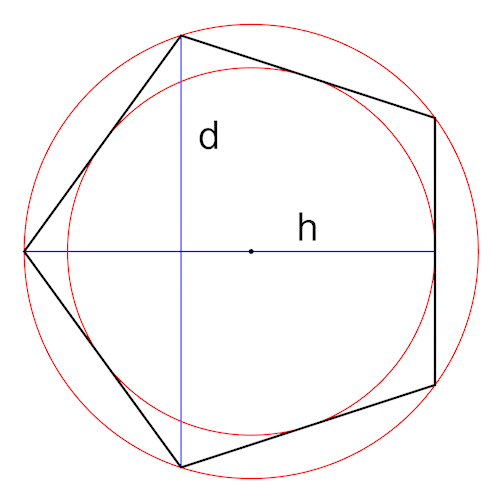
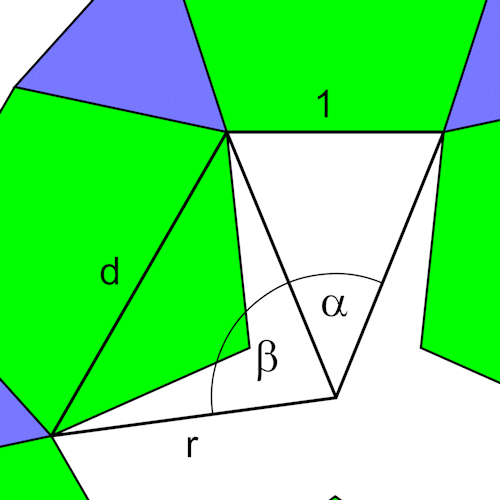
Für die Berechnung betrachten wir zuerst das Fünfeck (Kantenlänge = 1). Wichtig sind die Diagonale d, die Höhe h, der Inkreisradius ri und der Umkreisradius ru.
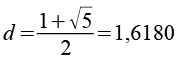
Die Diagonalen und Seite der Fünfecke bilden einen Ring.
Für die Berechnung betrachten wir die beiden gleichschenkligen Dreiecke.
Für die Winkel gilt.
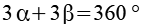
Für die beiden Winkel gilt.
Die beiden Winkel setzen wir in obige Gleichung ein.
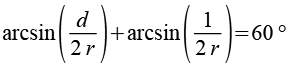
Um die Gleichung zu vereinfachen benutzen wir ein Additiostheorem aus einer Formelsammlung.
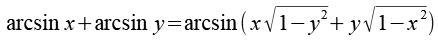
Damit erhalten wir.
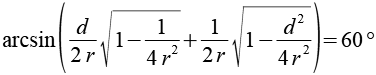
Auf beiden Seiten wenden wir die Sinusfunktion an.
Leider müssen wir diese Gleichung numerisch lösen: r = 1,32111921963914.
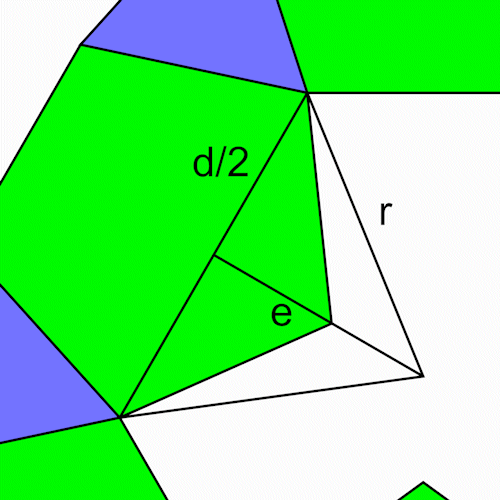
Den für den Polyederring nötigen Abstand e berechnen wir mit dem Pythagoras.
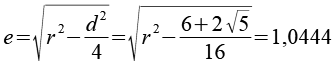
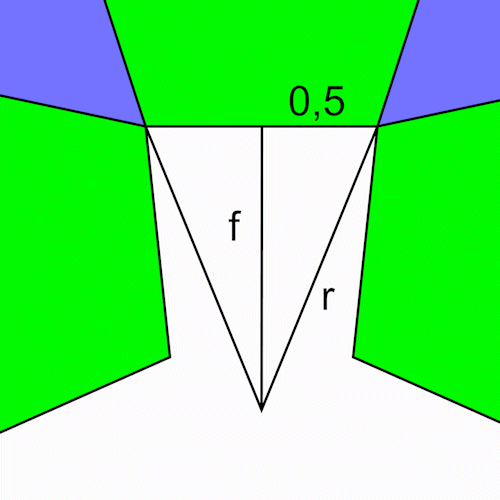
Den für den Polyederring nötigen Abstand f berechnen wir mit dem Pythagoras.
Da die 5-Eck Prismen verschoben und getreht werden müssen wählen wir als Ausgang eine günstige Positionen des 5-Eck Prismas und bestimmen die Koordinaten der Eckpunkte.
|
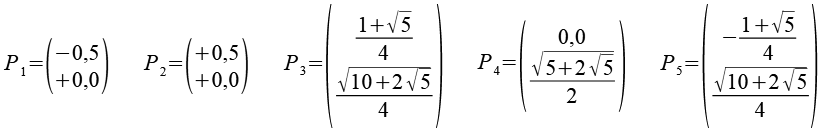
[zurück] | [Inhaltsverzeichnis] | [vor] | |