10.5. 6 6-Eck Antiprismen und 6 3-Eck Antiprismen
|
[zurück] | 10.5. 6 6-Eck Antiprismen und 6 3-Eck Antiprismen |
[vor] | |
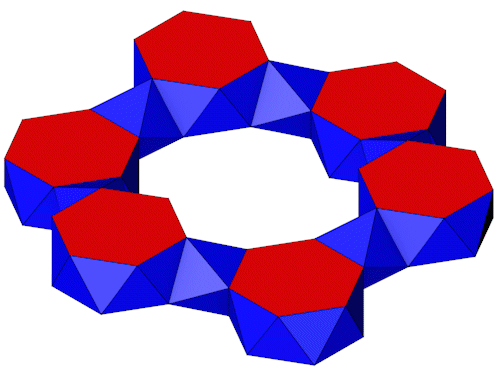
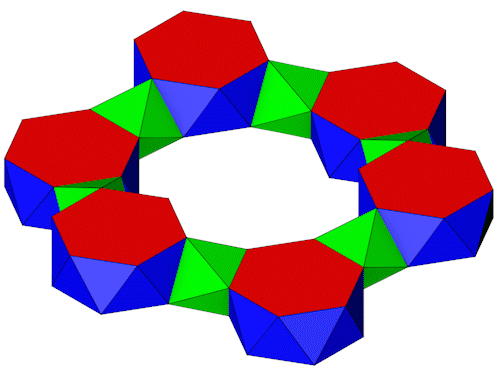
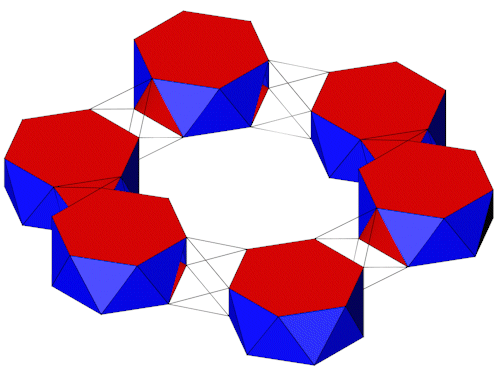
6 6-Eck Antiprismen lassen sich so in einem Sechseck anordnen das sie durch 6 3 Eck Antiprismen verbunden werden können.
 |
 |
| Anzahl Ecken | 72 |
| Anzahl Flächen | 96 Dreiecke 12 Sechsecke |
 |
 |
 |
 |
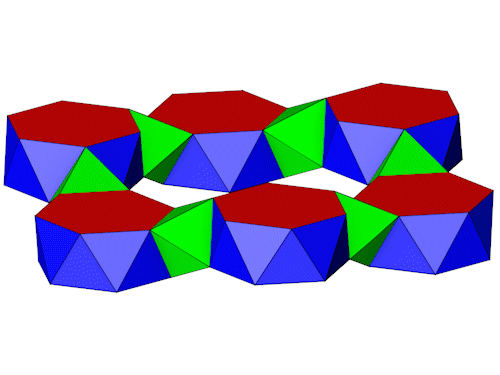
Die Seitenansichten.
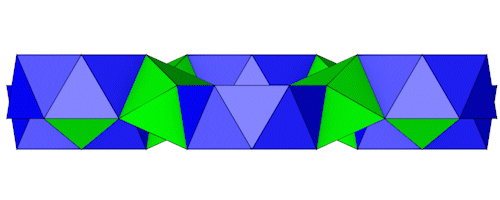
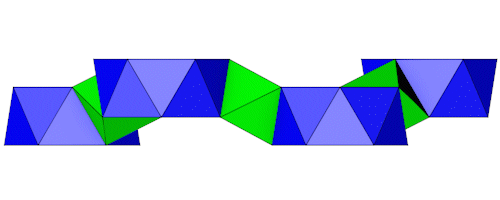
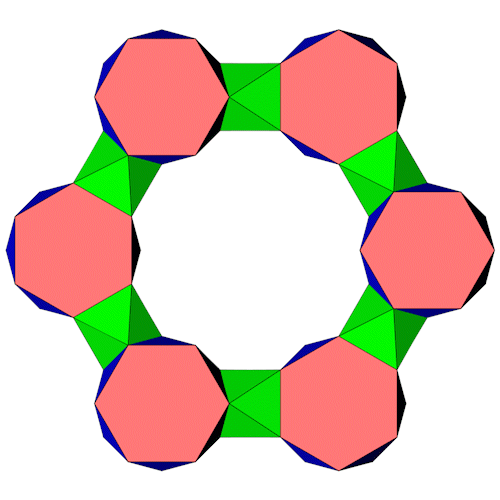
Die 6-Eck Antiprismen liegen nicht in einer Ebene, das macht die Berechnung etwas komplizierter. Es reicht aus die 6 6-Eck Antiprismen richtig zu positionieren, die Ecken der 3-Eck Antiprismen werden aus den Ecken der 6-Eck Antiprismen gebildet. Für die Berechnung benötigen wir ein paar Formeln, die Höhe des 3-Eck Antiprismas (hAP3), die Höhe des 6-Eck Antiprismas (hAP6), die Höhe des gleichseitigen Dreiecks (hD) und den Inkreisradius des Sechsecks (ri). Es gilt die Kantenlänge 1 für die Polygone.
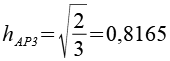
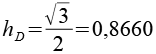
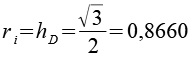
Das grüne Antiprisma bildet in der Vorderansicht eine Raute zwischen den parallelen Dreiecken der beiden 6 Eck Antiprismen. Die Kantenlänge der Raute ist hD.
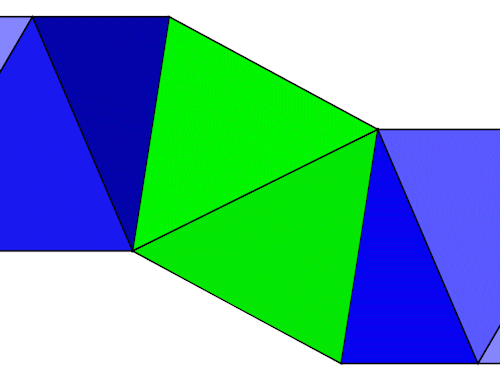
Für die Berechnung des Winkels alpha benutzen wir das rechwinklige Dreieck mit den Seiten hAP3 und hD.
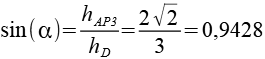
Aus alpha läßt sich der Winkel beta berechnen.
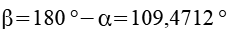
Der Winkel gamma läßt sich aus folgendem rechtwinkligen Dreieck berechnen.
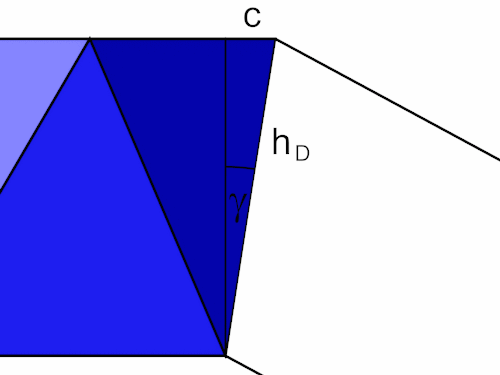
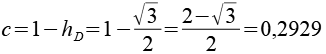
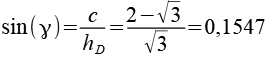
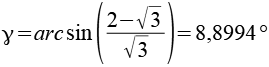
Für die Positionierung der 6-Eck Antiprismen müssen wir noch d und e berechnen, dabei greifen wir wieder auf ein rechtwinkliges Dreieck zurück. Der Winkel delta läßt sich leicht herleiten.
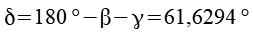
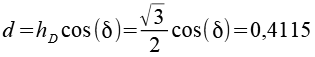
Jetzt lassen sich die Positionen der 6-Eck Antiprismen berechnen.
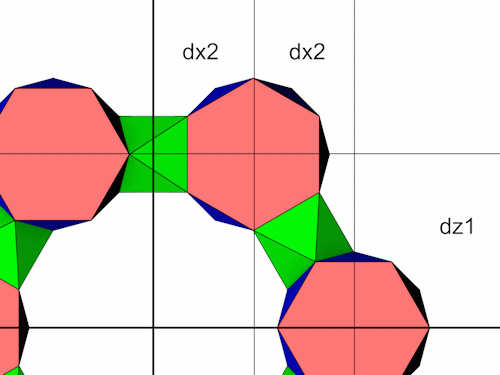
Mit
|
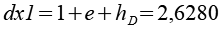
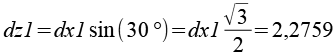
[zurück] | [Inhaltsverzeichnis] | [vor] | |