[zurück]

10.3. 4 Dodekaeder und 4 5-Eck Antiprismen

[vor]

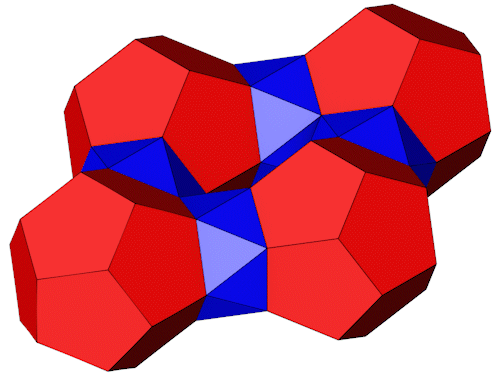
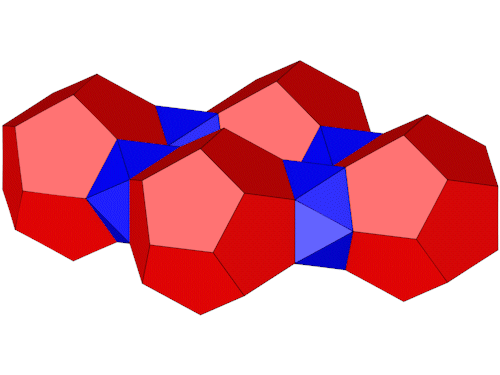
4 Dodekaeder lassen sich so anodnen dass sie mit 4 5-Eck Antiprismen verbunden werden können.

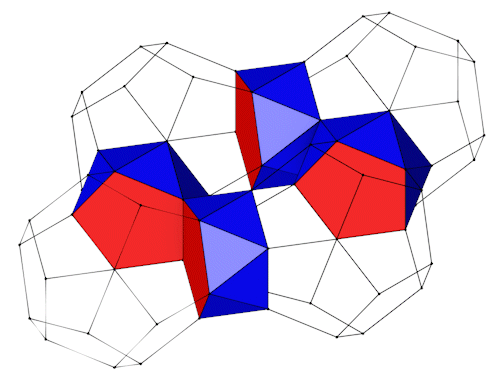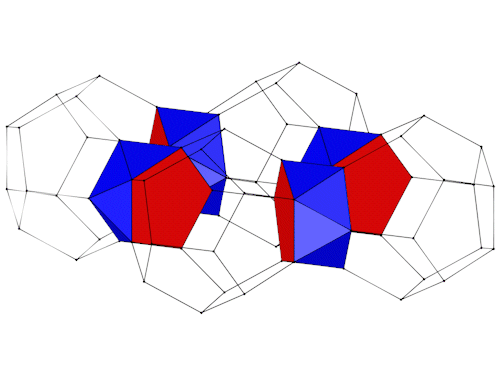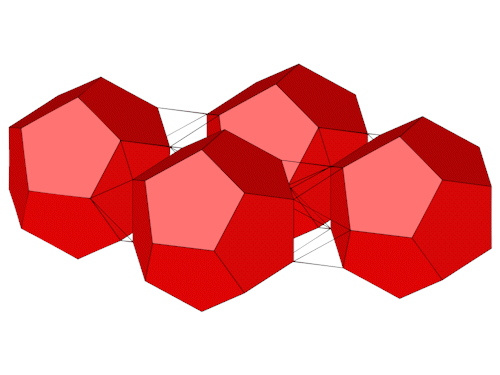
Die Seitenansichten.

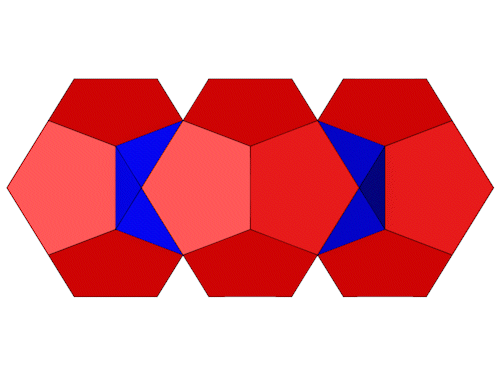
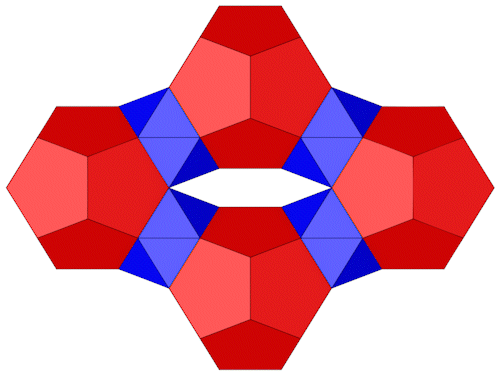
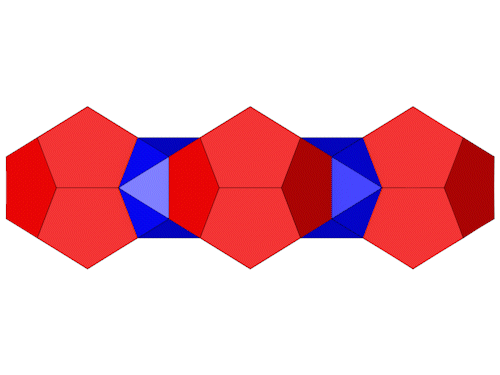
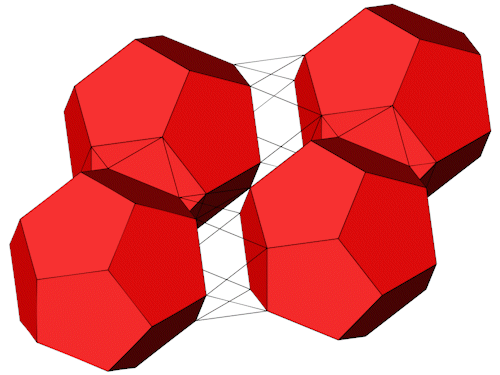
Die 4 roten Dodekaeder befinden sich auf den Eckpunkten einer Raute.

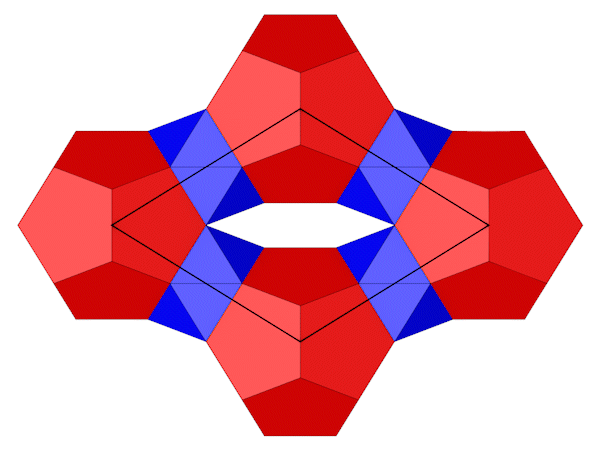
Einige Kanten (grün) liegen in der Draufsicht parallel zur Ebene, daraus lassen sich die Positionen der 4 Dodekaeder herleiten.

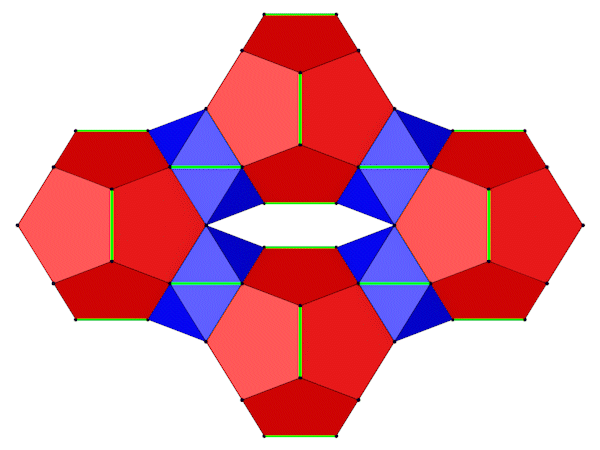
Für die Verschiebung der Dodekaeder vom Ursprung erhält man für d₁ und d₂.

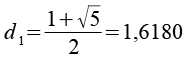
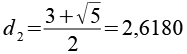
d₁ und d₂ bilden mit der Kantenlänge c der Raute ein rechtwinkliges Dreieck. Über den Pythagoras läßt sich c berechnen..

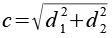
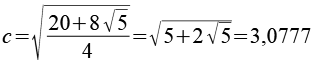
Die Kantenlänge c läßt sich auch über den Inkugelradius des Dosekaeders (r_i) und die Höhe des Antiprismas berechnen.

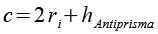
mit

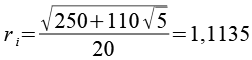
und

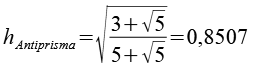
Für c erhält man dann.

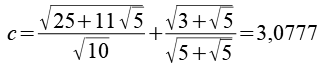
Beide Ansätze für die Berechnung von c führen über zwei sehr unterschiedliche Formeln zum gleichen Ergebnis. Also müsste sich die zweite Formel durch Umstellen in die erste Formel verwandeln lassen. Das erwies sich als schwieriger als gedacht.

Wir bringen die beiden Brüche auf einen Hauptnenner.

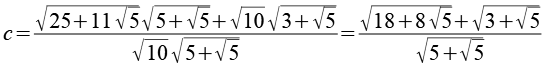
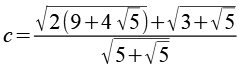
Die Wurzeln im Nenner sind ein Problem, jetzt führen wir den goldenen Schnitt phi ein. Dabei gilt

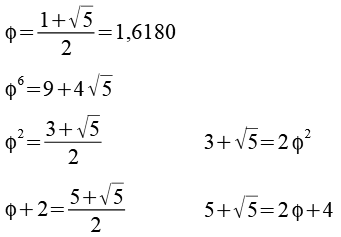
Für c erhalten wir dann

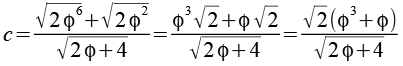
Jetzt werden beide Seiten quadriert

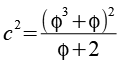
Jetzt ersetzen wir phi wieder

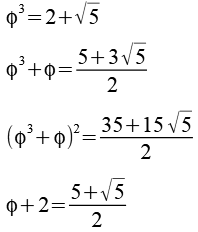
Für c² erhalten wir

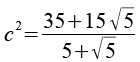
Zähler und Nenner multiplizieren wir mit Wurzel(5)

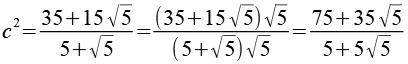
Den Faktor 5 kann man kürzen

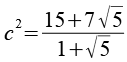
mit

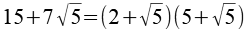
erhalten wir

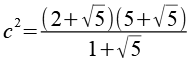
Jetzt setzen wir wieder phi ein

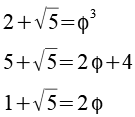
und erhalten

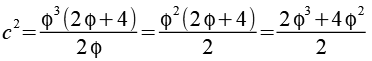
So konnte phi (und damit der Wurzelausdruck) aus dem Nenner herausgekürzt werden. Jetzt können wir phi wieder ersetzen

und erhalten

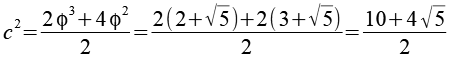
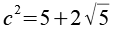
Jetzt müssen wir nur noch auf beiden Seite die Wurzel ziehen.

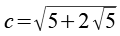
Damit ist der Beweis erbracht, sehr umständlich mit einem sehr ungewöhnlichen Lösungsweg, aber immerhin. Wahrscheinlich geht es auch einfacher aber einen anderen Weg habe ich nicht gesehen.

Es geht doch einfacher, wir multiplizieren Zähler und Nenner mit Wurzel(5).

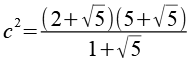
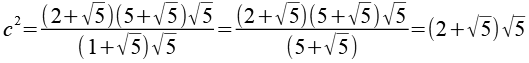
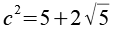
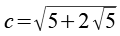
[zurück]

[Inhaltsverzeichnis]

[vor]