5.57. Rafiullah II Methode
|
[zurück] | 5.57. Rafiullah II Methode |
[vor] | |
Die Rafiullah II Fraktale [43] werden nach folgender Formel berechnet. Zur Berechnung wird neben der Funktion f(zn) auch die erste Ableitung f '(zn) benötigt.
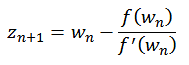
mit
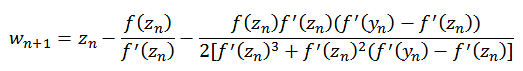
und
f(z) = z2 - 1
Nullstellen:
z1 = -1,0
z2 = 1,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Auch bei einem Polynom mit nur zwei Nullstellen gibt es eine Feinstruktur.
f(z) = z4 - 2 z2 + 1
Nullstellen:
z1,2 = -1,0
z3,4 = 1,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Bei doppelten Nullstellen gibt es keine Bereiche die zu keiner Nullstelle konvergieren.
Die folgende Abbildung zeigt einen Bereich real [0,3275 bis 0,3725] und imaginär [-0,0225 bis 0,0225].
f(z) = z3 - 1
Nullstellen:
z1 = -0,5 + 0,866025403784i
z2 = -0,5 - 0,866025403784i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z3 - z
Nullstellen:
z1 = 1
z2 = 0
z3 = -1
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = 1
z2 = -1
z3 = 2
z4 = -2
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [1,37 bis 1,81] und imaginär [0,25 bis 0,69].
Die folgende Abbildung zeigt einen Bereich real [-0,4 bis 0,4] und imaginär [-0,4 bis 0,4].
Die folgende Abbildung zeigt einen Bereich real [1,43 bis 1,61] und imaginär [-0,09 bis 0,09].
Die folgende Abbildung zeigt einen Bereich real [1,5435 bis 1,5450] und imaginär [-0,00075 bis 0,00075].
Die folgende Abbildung zeigt einen Bereich real [1,54401 bis 1,54432] und imaginär [-0,000155 bis 0,000155].
f(z) = z5 - 5 z3 + 4 z
Nullstellen:
z1 = -2
z2 = -1
z3 = 0
z4 = 1
z5 = 2
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z6 - 14 z4 + 49 z2 - 36
Nullstellen:
z1 = -3
z2 = -2
z3 = -1
z4 = 1
z5 = 2
z6 = 3
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [-4,0 bis 4,0] und imaginär [-4,0 bis 4,0]. Bei den folgenden Abbildungen habe ich die Farbe von z01 von türkis auf braun gewechselt.
Die folgende Abbildung zeigt einen Bereich real [-1,38 bis -1,55] und imaginär [-0,085 bis 0,085].
Die folgende Abbildung zeigt einen Bereich real [0,140 bis 0,148] und imaginär [-0,004 bis 0,004].
Die folgende Abbildung zeigt einen Bereich real [2,48 bis 2,72] und imaginär [-0,12 bis 0,12].
Um zu anderen interessanten Bildern zu kommen habe ich die Formel ein bischen modifiziert. Dabei hatte ich folgender Formel verwendet.
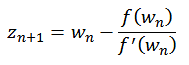
mit
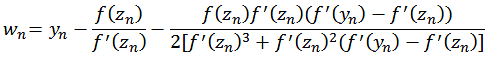
und
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = 1
z2 = -1
z3 = 2
z4 = -2
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [0,276 bis 0,309] und imaginär [-0,0165 bis 0,0165].
Die folgende Abbildung zeigt einen Bereich real [0,2865 bis 0,2955] und imaginär [-0,0045 bis 0,0045].
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |