| [zurück] | 4.11. Exotische Juliamengen |
[vor] |
Diese Julia Fraktale habe ich auf der Webseite von Michael Becker [35] gefunden. Sie haben mich sehr fasziniert aber ich habe lange keinen Weg gefunden sie zu berechnen. Nun hat es über die "Distance estimation" Methode funktioniert.
Funktion 1Diese Julia Menge wird nach folgender Formel berechnet.
![]()
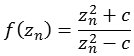
Für die Berechnung der "Distance estimation" Methode wird die erste Ableitung benötigt, da es sich um eine gebrochen rationale Funktion handelt müssen wir die Quotientenregel anwenden.
![]()
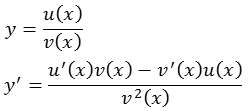
Damit erhalten wir.
![]()
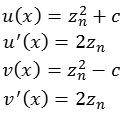
![]()
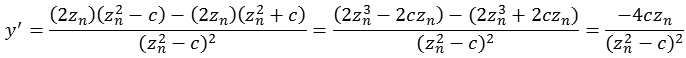
![]()
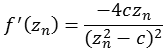
Die folgende Abbildung zeigt einen Bereich real [-1,7 bis 1,7] und imaginär [-1,7 bis 1,7] mit c = 0,7.
Funktion 2Diese Julia Menge wird nach folgender Formel berechnet.
![]()
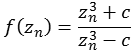
![]()
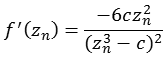
Die folgende Abbildung zeigt einen Bereich real [-1,4 bis 1,4] und imaginär [-1,4 bis 1,4] mit c = 0,45.
Funktion 3Diese Julia Menge wird nach folgender Formel berechnet.
![]()
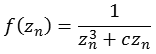
![]()
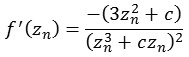
Die folgende Abbildung zeigt einen Bereich real [-2,8 bis 2,8] und imaginär [-2,8 bis 2,8] mit c = -2 + 3i. Dies ist eine der schönsten Juliamengen die ich kenne.
Die folgende Abbildung zeigt einen Bereich real [-2,2 bis 2,2] und imaginär [-2,2 bis 2,2] mit c = -1,7 + 2,4i.
Funktion 4Diese Julia Menge wird nach folgender Formel berechnet.
![]()
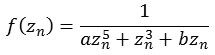
![]()
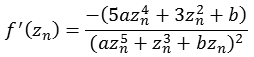
Die folgende Abbildung zeigt einen Bereich real [-2,8 bis 2,8] und imaginär [-2,8 bis 2,8] mit a = 0,15 + 0,15i und b = -3 + 3i. Dies ist eine der schönsten Juliamengen die ich kenne.
Funktion 5Diese Julia Menge wird nach folgender Formel berechnet.
![]()
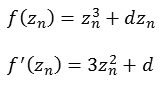
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Die folgende Abbildung zeigt einen Bereich real [-0,23 bis -0,03] und imaginär [0,40 bis 0,60].
Die folgende Abbildung zeigt einen Bereich real [-0,15 bis -0,35] und imaginär [0,125 bis 0,325].
Funktion 6Diese Julia Menge wird nach folgender Formel berechnet.
Die folgende Abbildung zeigt einen Bereich real [-1,5 bis 1,5] und imaginär [-1,5 bis 1,5].
Funktion 7Diese Julia Menge wird nach folgender Formel berechnet.
![]()
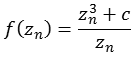
![]()
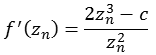
Die folgende Abbildung zeigt einen Bereich real [-1,1 bis 1,1] und imaginär [-1,1 bis 1,1] mit c = 0,01.
Bei der folgende Abbildung habe ich den Algorithmus etwas verändert. Normalerweise wird die Bildebene gleichmäßig gerastert und für jeden Rasterpunkt wird entschieden ob er gezeichnet wird oder nicht. Das führt in diesem Fall zu sehr dünnen Strukturen, bei etwas größeren Rasterpunkten läßt sich das vermeiden.
Funktion 8Diese Julia Menge wird nach folgender Formel berechnet.
![]()

![]()
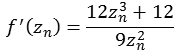
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-2,0 bis 2,0].
Funktion 9Dieses "Bubble Bath Julia Fraktal" habe ich hier [81] gefunden, es wird nach folgender Formel berechnet.
![]()
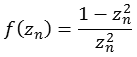
![]()
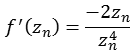
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Bei der folgende Abbildung habe ich zusätzlich einen "Binary decomposition" eingefügt.
Funktion 10Diese Julia Menge wird nach folgender Formel berechnet.
![]()
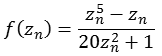
![]()
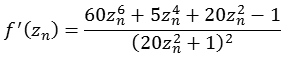
Die folgende Abbildung zeigt einen Bereich real [-5,0 bis 5,0] und imaginär [-5,0 bis 5,0].
Funktion 11Diese Julia Menge wird nach folgender Formel berechnet.
![]()
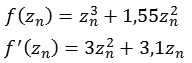
Die folgende Abbildung zeigt einen Bereich real [-5,0 bis 5,0] und imaginär [-5,0 bis 5,0].
Funktion 13Diese Julia Menge wird nach folgender Formel berechnet.
![]()
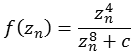
![]()
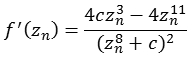
Die folgende Abbildung zeigt einen Bereich real [-5,0 bis 5,0] und imaginär [-5,0 bis 5,0].
Funktion 14Diese Julia Menge wird nach folgender Formel berechnet.
![]()
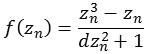
![]()
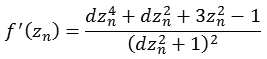
Die folgende Abbildung zeigt einen Bereich real [-7,0 bis 7,0] und imaginär [-7,0 bis 7,0].
Die folgende Abbildung zeigt einen Bereich real [-5,0 bis 5,0] und imaginär [-5,0 bis 5,0]. Leider fehlen hier die Spiralstrukturen am Ende der vier Ausläufer, siehe Quelle [35].
Funktion 15Diese Julia Menge wird nach folgender Formel berechnet.
![]()
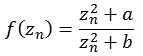
![]()
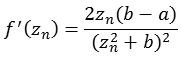
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-2,0 bis 2,0]. Leider fehlen hier die Spiralstrukturen am Ende der vier Ausläufer, siehe Quelle [35].
Funktion 16Diese Julia Menge wird nach folgender Formel berechnet.
![]()
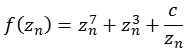
![]()
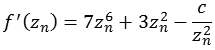
![]()
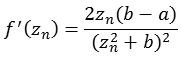
Die folgende Abbildung zeigt einen Bereich real [-1,0 bis 1,0] und imaginär [-1,0 bis 1,0]. Leider ist es mir auch hier nicht gelungen die Feinstruktur richtig darzustellen, siehe Quelle [35].
Funktion 17Diese Julia Menge wird nach folgender Formel berechnet.
![]()
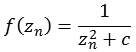
![]()
![]()
Die folgende Abbildung zeigt einen Bereich real [-2,0 bis 2,0] und imaginär [-2,0 bis 2,0].
Funktion 18Diese Julia Menge wird nach folgender Formel berechnet.
![]()
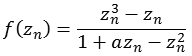
![]()
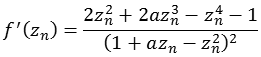
Die folgende Abbildung zeigt einen Bereich real [-8,0 bis 8,0] und imaginär [-8,0 bis 8,0].
| [zurück] | [Inhaltsverzeichnis] | [vor] |