5.24. Jarratt I Methode
|
[zurück] | 5.24. Jarratt I Methode |
[vor] | |
Die Jarratt I Fraktale [9, 52, 59] werden nach folgender Formel berechnet. Zur Berechnung wird neben der Funktion f(zn) auch die erste Ableitung f '(zn) benötigt. Hier habe ich mit yn etwas die Schreibweise der Formeln geändert.
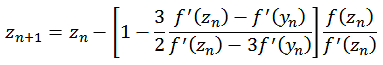
mit
f(z) = z2 - 1
Nullstellen:
z1 = -1,0
z2 = 1,0
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5]. Bei einem Polynom mit nur zwei Nullstellen ist das Bild trivial.
f(z) = z3 - 1
Nullstellen:
z1 = -0,5 + 0,866025403784i
z2 = -0,5 - 0,866025403784i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = 1
z2 = -1
z3 = 2
z4 = -2
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [-0,25 bis 0,25] und imaginär [-0,25 bis 0,25].
Die folgende Abbildung zeigt einen Bereich real [1,515 bis 1,585] und imaginär [-0,035 bis 0,035].
Die folgende Abbildung zeigt einen Bereich real [1,5561 bis 1,5573] und imaginär [-0,0006 bis 0,0006].
Die folgende Abbildung zeigt einen Bereich real [1,545 bis 1,650] und imaginär [0,410 bis 0,515].
Durch einen Schreibfehler war die Formel zuerst fehlerhaft, das Ergebnis war allerdings sehr interessant und so habe ich mit der falschen Formel auch ein paar Bilder berechnet.
mit
f(z) = z4 - 5 z2 + 4
Nullstellen:
z1 = 1
z2 = -1
z3 = 2
z4 = -2
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
Die folgende Abbildung zeigt einen Bereich real [-0,55 bis 0,55] und imaginär [-0,55 bis 0,55].
Die folgende Abbildung zeigt einen Bereich real [0,17 bis 0,206] und imaginär [-0,018 bis 0,018].
f(z) = z3 - 1
Nullstellen:
z1 = -0,5 + 0,866025403784i
z2 = -0,5 - 0,866025403784i
z3 = 1,0 + 0,0i
Die folgende Abbildung zeigt einen Bereich real [-2,5 bis 2,5] und imaginär [-2,5 bis 2,5].
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |