| [zurück] | 4.8. Collatz Fraktal |
[vor] |
Das Collatz-Problem [61, 62, 63] geht auf den Mathematiker Lothar Collatz (1910 - 1990) zurück. Bei dem Problem geht es um Zahlenfolgen, die nach einem einfachen Bildungsgesetz konstruiert werden:
![]()

![]()

Begonnen wird mit einer natürlichen Zahl n>0, wenn n gerade ist wird die Zahl durch 2 geteilt, wenn n ungerade ist wird sie
mit 3 multipliziert und es wird 1 addiert. Mit der erhaltenen Zahl wir dieser Vorgang wiederholt. Für den Startwert 13 erhält
man die Folge
![]()

Die Berechnung habe ich für die Zahlen 1 bis 100 durchgeführt. Je nach Startwert dauert es unterschiedlich lange bis die Folge den Wert 1 erreicht. Diesen Zusammenhang habe ich in folgendem Diagramm dargestellt.
Beim Startwert 97 hat die Folge 119 Glieder. Dabei treten unterschiedlich große Zahlen auf, diesen Zusammenhang habe ich in folgendem Diagramm dargestellt. Sie zeigt den Maximalwert als Funktion des Startwertes.
Die nächste Abbildung zeigt aller Glieder der Folge für den Startwert 27.
Mit dem Collatz Problem lassen sich aber auch fraktale Grafiken erzeugen. Dazu benutzen wir folgende Formel.
![]()
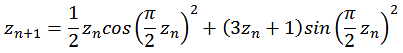
Durch die trigonometrischen Funktionen erfolgt die Trennung in gerade und ungerade Zahlen.
![]()
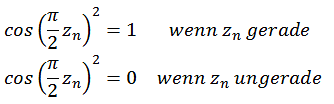
![]()
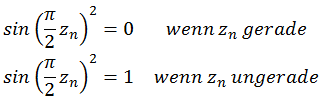
Sie läßt sich auch etwas vereinfachen, die Herleitung befindet sich am Ende dieser Seite.
![]()
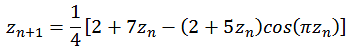
Die folgende Abbildung zeigt einen Bereich real [-10 bis 10] und imaginär [-2 bis 2].
Die folgende Abbildung zeigt einen Bereich real [-1,1 bis 0,9] und imaginär [-1,0 bis 1,0].
Die folgende Abbildung zeigt einen Bereich real [-0,7625 bis -0,6625] und imaginär [-0,05 bis 0,05].
Die folgende Abbildung zeigt einen Bereich real [1,5 bis 2,5] und imaginär [-0,5 bis 0,5].
Die folgende Abbildung zeigt einen Bereich real [2,5 bis 3,5] und imaginär [-0,5 bis 0,5].
Die folgende Abbildung zeigt einen Bereich real [3,5 bis 4,5] und imaginär [-0,5 bis 0,5].
Die folgende Abbildung zeigt einen Bereich real [3,85 bis 3,95] und imaginär [0,035 bis 0,135].
Die folgende Abbildung zeigt einen Bereich real [3,898 bis 3,905] und imaginär [0,085 bis 0,092].
Die folgende Abbildung zeigt einen Bereich real [3,90142 bis 3,90172] und imaginär [0,08843 bis 0,08873].
Die folgende Abbildung zeigt einen Bereich real [4,50 bis 5,50] und imaginär [-0,50 bis 0,50].
Die folgende Abbildung zeigt einen Bereich real [5,50 bis 6,50] und imaginär [-0,50 bis 0,50].
Die folgende Abbildung zeigt einen Bereich real [6,50 bis 7,50] und imaginär [-0,50 bis 0,50].
Die folgende Abbildung zeigt einen Bereich real [7,178 bis 7,190] und imaginär [-0,006 bis 0,006].
Die folgende Abbildung zeigt einen Bereich real [7,18285 bis 7,18355] und imaginär [-0,00035 bis 0,00035].
Die folgende Abbildung zeigt einen Bereich real [7,1834035 bis 7,1834135] und imaginär [0,000121 bis 0,000131].
Die folgende Abbildung zeigt einen Bereich real [7,50 bis 8,50] und imaginär [-0,50 bis 0,50].
Die folgende Abbildung zeigt einen Bereich real [7,89 bis 8,10] und imaginär [-0,105 bis 0,105].
Mit Hilfe der Potenzen der Winkelfunktionen läßt sich die Formel vereinfachen.
![]()
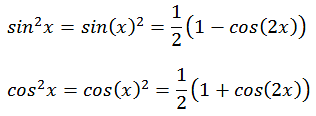
Durch Einsetzen in die obige Gleichung erhält man.
![]()

| [zurück] | [Inhaltsverzeichnis] | [vor] |