| [zurück] | 4.9. Apollonian Gasket |
[vor] |
Der Apollonian Gasket [77, 78, 79] wird nach folgender Formel berechnet.
![]()
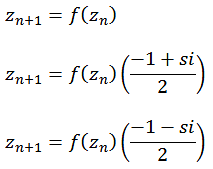
mit
![]()
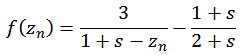
und
![]()
![]()
Die ersten drei Gleichungen werden statistisch zufällig nacheinander angewendet. Der Apollonian Gasket entsteht dann als Punktwolke.
Man kann den Apollonian Gasket auch aus Kreisen zusammensetzen.
Die Radien der Kreise lassen sich nach dem Satz von Descartes [80] berechnen. Für Kreise, die einander berühren, gilt folgende Gleichung.
| A1 |
k bedeutet die Krümmung eines Kreises und kann aus dem Radius r berechnet werden
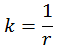 |
A2 |
Sind drei Kreise gegeben so läßt sich der Radius bzw. die Krümmung des vierten Kreises berechnen.
| A3 |
Die folgende Abbildung veranschaulicht den Zusammenhang.
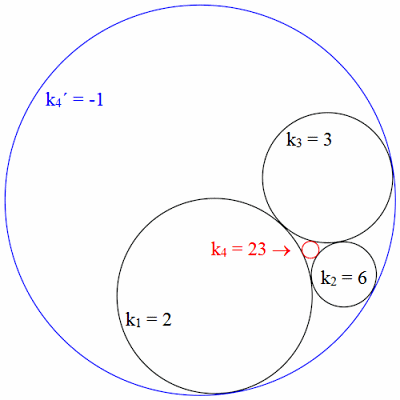
Durch die Wurzel gibt es für k4 zwei Lösungen, den kleinen Kreis k4 = 23 und den großen Kreis k4 = -1. Der große Kreis umschließt die drei Kreise aussen.
Gleichung A3 möchte ich im folgenden aus Gleichung A1 herleiten. Zuerst nehmen wir die linke Seite von Gleichung 1 und multiplizieren die Klammer aus.
| A4 | ||
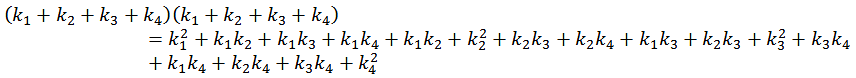 |
A5 |
Für die linke Seite von Gl. A1 erhalten wir so.
| A6 |
Gl. A6 können wir in Gl. A1 einsetzen.
| A7 |
Gl. A7 läßt sich vereinfachen.
| A8 | ||
| A9 |
Bei Gl. A9 handelt es sich um eine quadratische Gleichung.
| A10 |
Die Lösung der quadratischen Gleichung entnehmen wir der Literatur.
| A11 | ||
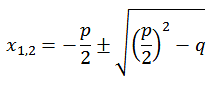 |
A12 |
Für die beiden Konstanten p und q erhalten wir.
| A13 | ||
| A14 |
Mit p und q kommen wir der Lösung ein Stück weiter.
| A15 | ||
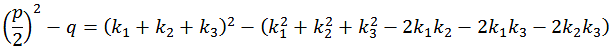 |
A16 |
Multiplizieren wir einen Teil von Gl. A16 aus.
| A17 | ||
| A18 | ||
| A19 |
Gl. A19 setzten wir wieder in Gl. A16 ein.
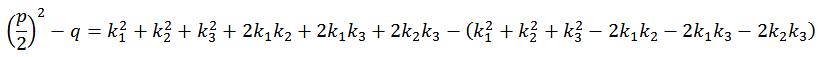 |
A20 |
Gl. A20 können wir weiter vereinfachen.
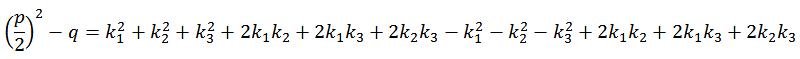 |
A21 | |
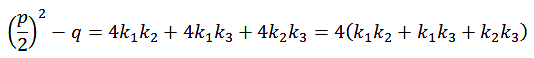 |
A22 |
Für die Lösung der quadratischen Gleichung setzten Gl. A15 und Gl. A22 ij Gl. A12 ein.
| A23 | ||
| A24 |
Mit Gl. 24 erhalten wir Gl. A3, was zu beweisen war.
| [zurück] | [Inhaltsverzeichnis] | [vor] |