| [zurück] | 3.7. zn+1 = znm + c/znm |
[vor] |
Diese Fraktale werden nach folgender Formel berechnet.
![]()

Je nach Exponent m bilden sich große und viele kleine Apfelmännchen. Bei diesen Fraktalen hatte ich große Probleme den geigneten Startwert z0 zu finden, die Lösung habe ich dann in der Literatur gefunden. Der Startwert ist abhängig von der der Konstanten c und der Potenz m, d.h. z0 = c1/(2*m).
m = 2
![]()

Die folgende Abbildung zeigt einen Bereich real [-0,5 bis 0,2] und imaginär [-0,3 bis 0,3]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (500, 30, 15 und 10).
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [-0,23 bis -0,08] und imaginär [-0,2 bis -0,05]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (1000, 50, 23 und 13).
Die folgende Abbildung zeigt einen Ausschnitt des ersten Bildes im Bereich real [0,033 bis 0,083] und imaginär [0,175 bis 0,225]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (1000, 60, 25 und 15).
Die folgende Abbildung zeigt einen Ausschnitt des ersten Bildes im Bereich real [-0,02 bis 0,02] und imaginär [-0,02 bis 0,02]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (1000, 50, 35 und 15).
m = 3
![]()
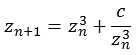
Die folgende Abbildung zeigt einen Bereich real [-0,4 bis 0,4] und imaginär [-0,4 bis 0,4]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (500, 30, 15 und 8).
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [0,0 bis 0,2] und imaginär [-0,1 bis -0,1]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (1000, 40, 15 und 8).
Die folgende Abbildung zeigt einen Ausschnitt des ersten Bildes im Bereich real [0,092 bis 0,142] und imaginär [0,1667 bis 0,2167]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (1000, 30, 15 und 10).
Die folgende Abbildung zeigt einen Ausschnitt des ersten Bildes im Bereich real [-0,08 bis 0,08] und imaginär [-0,06 bis 0,06]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (1000, 30, 15 und 8).
m = 4
![]()
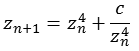
Die folgende Abbildung zeigt einen Bereich real [-0,4 bis 0,4] und imaginär [-0,4 bis 0,4]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (250, 20, 10 und 6).
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [0,05 bis 0,25] und imaginär [-0,1 bis -0,1]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (1000, 30, 15 und 8).
m = 5
![]()
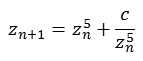
Die folgende Abbildung zeigt einen Bereich real [-0,25 bis 0,25] und imaginär [-0,25 bis 0,25]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (1000, 20, 8 und 5).
Die folgende Abbildung zeigt einen Ausschnitt des letzten Bildes im Bereich real [0,08 bis 0,28] und imaginär [-0,1 bis -0,1]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (1000, 20, 8 und 5).
m = 6
![]()
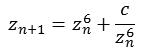
Die folgende Abbildung zeigt einen Bereich real [-0,3 bis 0,3] und imaginär [-0,3 bis 0,3]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (500, 15, 7 und 5).
m = 7
![]()

Die folgende Abbildung zeigt einen Bereich real [-0,3 bis 0,3] und imaginär [-0,3 bis 0,3]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (500, 15, 7 und 5).
m = 8
![]()

Die folgende Abbildung zeigt einen Bereich real [-0,3 bis 0,3] und imaginär [-0,3 bis 0,3]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (500, 15, 8 und 5).
m = 9
![]()
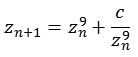
Die folgende Abbildung zeigt einen Bereich real [-0,3 bis 0,3] und imaginär [-0,3 bis 0,3]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (500, 13, 6 und 5).
m = 10
![]()
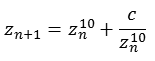
Die folgende Abbildung zeigt einen Bereich real [-0,3 bis 0,3] und imaginär [-0,3 bis 0,3]. Dargestellt sind vier Ebenen mit unterschiedlicher Iterationstiefe (500, 10, 5 und 4).
| [zurück] | [Inhaltsverzeichnis] | [vor] |