2.129. Rekurrenzplots
|
[zurück] | 2.129. Rekurrenzplots |
[vor] | |
Rekurrenzplots sind eine moderne Methode der nichtlinearen Datenanalyse [127, 128, 129, 130, 131, 132].
Dabei wird eine Datenreihe f(t) in einem Koordinatensystem sowohl auf der x als auch auf der y Achse aufgetragen. Alle
Werte werden miteinander verglichen, unterschreitet ihre Differenz einen bestimmten Wert Delta wird an dieser Stelle ein Punkt
gesetzt. Das so erzeugte Muster ist der Rekurrenzplot. Als Beispiel nehmen wir eine Periode einer Sinusschwingung. Die
Amplitude ist so gross gewählt um nicht so kleine Werte für Delta zu erhalten.
Das passt hier nicht ganz zum Thema Attraktoren aber so lassen sich z.T sehr hübsche Muster erzeugen.
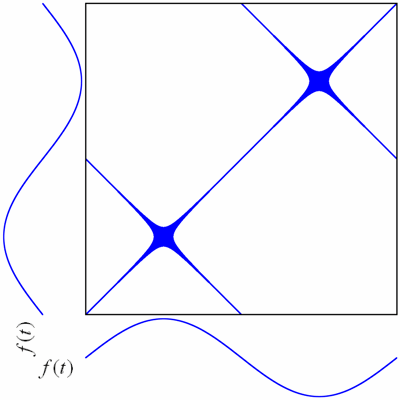
Rekurrenzplot am Beispiel der Sinuskurve
Die folgenden Abbildungen unterscheiden sich nur im Delta Wert. Je größer der Delta Wert desto mehr Punkte werden dargestellt und um so gröber wird die Struktur. Die Unterteilung bzw. die Anzahl der Punkte auf den Zeitachsen beträgt N=2000. N ist jeweils in die Formeln integriert so dass N im Plugin frei gewählt werden kann ohne den Kurvenverlauf zu verändern.
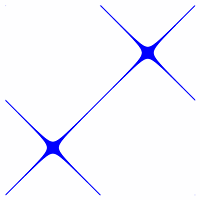
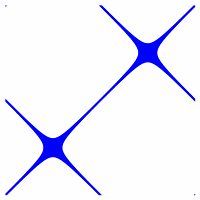
Delta = 0,25
Delta = 1,00Delta = 2,50
Werden mehrere Perioden dargestellt ist die Struktur des Rekurrenzplots feiner unterteilt (Delta = 1).
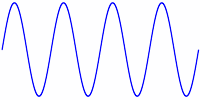
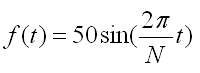
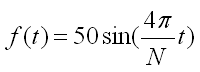
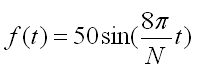
eine Periodezwei Periodenvier Perioden
Die verschiedenen trigonometrischen Funktionen ergeben unterschiedliche Rekurrenzplots (Delta = 1).
SinusCosinusTangens
Zwei Sinusschwingen mit unterschiedlicher Frequenz werden addiert.
Delta = 1
Delta = 2
Werden zwei Sinusschwingen mit geringfügig unterschiedlicher Frequenz addiert erhält man eine Schwebung.
Delta = 2
Schwebung mit zwei Perioden.
Delta = 5
Addition zweier trigonometrischer Funktionen mit unterschiedlicher Frequenz.
Delta = 2
Delta = 2
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |