| [zurück] | Watt Geradführung |
[vor] |
Die Watt Geradführung bzw. das Watt Gestänge wurde von James Watt (1736 - 1819) erfunden. Sie diente zur Führung des Kolbens seiner Dampfmaschine.
Die Animation erfolgt wie bei der Doppelschwinge.
Die Stäbe haben folgende Längen. Die Stäbe b und d sind gleich lang.
| a = 10,77 | ||
| b = 5 | ||
| c = 4 | ||
| d = 5 |
Die Länge des Stabes a wird aus den Längen der anderen Stäbe berechnet, dazu kommen wir aber später.
In dieser Darstellung befinden sich beide Lager nicht gemeinsam auf der x-Achse. Bei der Berechnung der Winkel wird das aber vorausgesetzt (siehe Gelenkviereck). Dieses Problem können wir umgehen wenn wir erst das fertige Modell in diese Position drehen (um den Winkel beta).
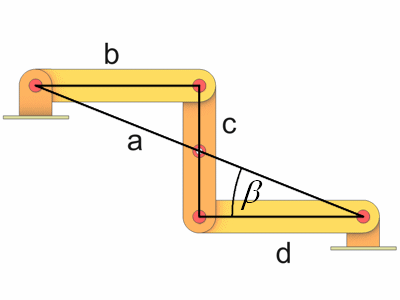
Der Winkel beta läßt sich leicht aus dem rechtwinkligen Dreieck berechnen.
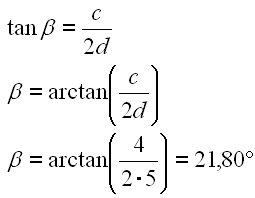 |
Bei dieser Gelegenheit können wir auch die Länge des Stabes a herleiten. Dazu verwenden wir wieder das rechtwinklige Dreieck und wenden den Satz des Pythagoras an.
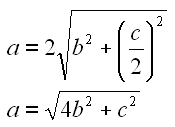 |
Ohne die Drehung haben wir wieder ein normales Gelenkviereck.
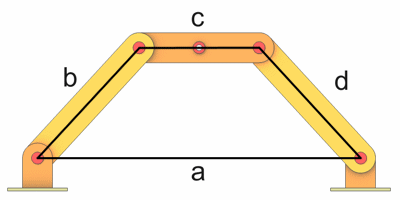
Da es sich um eine Doppelschwinge handelt müssen wir noch die Tot- bzw. Grenzlagen berechnen.
Berechnen wir zuerst phi1 von Totlage 1.
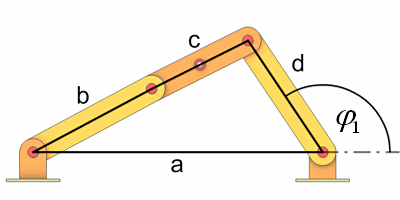
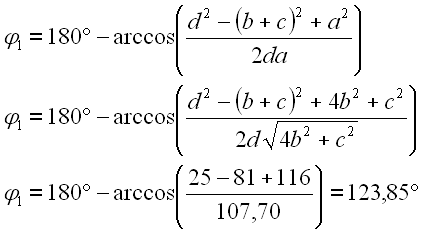 |
Berechnen wir phi2 von Totlage 2.
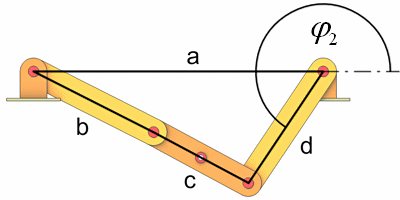
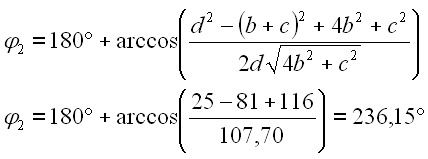 |
Die Koppelkurve besteht aus zwei Teilen (rot und blau). Für jede Kurve ist Gl. 43 aus dem Gelenkviereck zuständig.
 |
||
 |
Für jeden Winkel phi der Kurbel existieren zwei Stellungen der Schwinge.
Die Kreisbögen der Kurbel und der Schwinge schmiegen sich exakt an die Koppelkurve an.
Download C4D Datei (Release 11) : Watt.zip
| [zurück] | [Inhaltsverzeichnis] | [vor] |