| [zurück] | Gelenkviereck |
[vor] |
Ein Gelenkviereck bzw. ein viergliedriges Koppelgetriebe besteht aus vier in einer Ebene liegenden drehbar verbundenen Stäben.
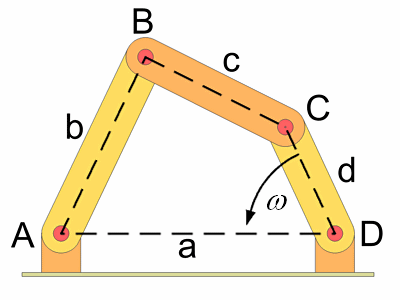
Die vier Stäbe werden wie folgt definiert.
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Die vier Stäbe werden wie folgt bezeichnet.
| a : Gestell | ||
| b : Schwinge | ||
| c : Koppel | ||
| d : Kurbel |
Von den vier Stäben wird das Gestell a festgehalten und die Kurbel d wird angetrieben. Die Bewegung wird von der Koppel c
auf die Schwinge b übertragen.
Die Berechnung der Winkel habe ich aus dem Buch Maschinendynamik von Prof. Uwe Hollburg übernommen, auf diesen Lösungsansatz
wäre ich nie selbst gekommen.
| Prof. Uwe Hollburg |
| Maschinendynamik |
| Oldenbourg Verlag |
| ISBN: 978-3-486-57898-0 |
| Google Books |
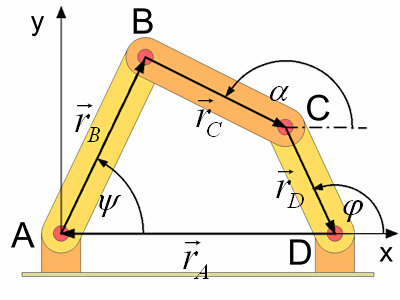
Die einzelnen Stäbe werden als Vektoren aufgefaßt. Die Winkel werden wie folgt bezeichnet.
| phi : Kurbeldrehwinkel | ||
| alpha : Koppeldrehwinkel | ||
| psi : Schwingendrehwinkel |
Die Vektoren werden wie folgt definiert.
| 5 | ||
| 6 | ||
| 7 | ||
| 8 |
Die Winkel werden von der positiven x-Achse aus gezählt. Für jede beliebige Getriebestellung gilt die Schleifengleichung.
| 9 |
Jetzt setzen wir Gl. 5 bis Gl. 8 in Gl. 9 ein und schreiben sie in Koordinaten.
| 10 | ||
| 11 |
Wir haben jetzt 2 Gleichungen mit 2 Unbekannten, das ist also lösbar. Der Lösungsweg ist aber durchaus kompliziert und birgt
viele Fehlerquellen. Den exakten Lösungsweg habe ich daher in Anhang A ausgegliedert damit es hier
nicht zu unübersichtlich wird.
Um die Gleichungen überprüfen zu können benötigen wir ein komplettes Zahlenbeispiel. Ich habe dieses Gelenkviereck in Cinema
nachgebaut und so die unbekannten Winkel bestimmt. Die Stäbe und Winkel haben folgende Werte.
| a = 7 | ||
| b = 5 | ||
| c = 4 | ||
| d = 3 | ||
| phi = 115° | ||
| alpha = 153,38° | ||
| psi = 64,45° |
Für die Berechnung benötigen wir noch einige Formeln die man in jeder guten Formelsammlung finden kann. Diese Formeln habe ich in Anhang B zusammengefaßt.
Um die Richtigkeit des Ansatzes zu überprüfen setzen wir die Zahlenwerte in Gl. 10 und Gl. 11 ein (siehe Anhang A1).
Um den Koppeldrehwinkel alpha eliminieren zu können stellen wir Gl. 10 und Gl. 11 um.
| 12 | ||
| 13 |
Gl. 12 und Gl. 13 werden jetzt quadriert und addiert (siehe Anhang A2). Nach einigen Umstellungen erhalten wir Gl. 14.
 |
14 |
Für die Berechnung des Koppeldrehwinkels alpha müssen wir den Schwingendrehwinkel psi eliminieren. Dazu stellen wir Gl. 10 und Gl. 11 entsprechend um.
| 15 | ||
| 16 |
Gl. 15 und Gl. 16 werden jetzt quadriert und addiert (siehe Anhang A3). Nach einigen Umstellungen erhalten wir Gl. 17.
 |
17 |
Gl. 17 weicht in einigen Punkten (Vorzeichen) von Gl. 2.126 aus dem Buch Maschinendynamik ab. Dort gibt es offensichtlich ein paar Druckfehler.
Um Gl. 14 und Gl. 17 zu vereinfachen führen wir die Konstanten k1 bis k5 ein.
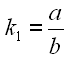 |
18 | |
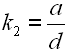 |
19 | |
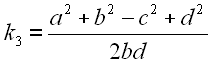 |
20 | |
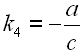 |
21 | |
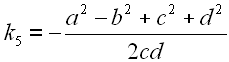 |
22 |
Mit Hilfe dieser Konstanten erhalten wir aus Gl. 14 und Gl. 17 die Gleichungen 23 und 24.
| 23 | ||
| 24 |
In diese beiden Gleichungen setzen wir wieder Gleichung B2 ein.
| 25 | ||
| 26 |
Wir haben wieder 2 Gleichungen mit je einer Unbekannten. Fangen wir mit Gl. 25 an. Sie nach psi aufzulösen ist aufgrund der trigonometrischen Funktionen nicht ohne weiteres möglich. Dazu müssen wir einen Trick anwenden. Wir ersetzen den Sinus und den Cosinus durch Gleichung B3 und B4.
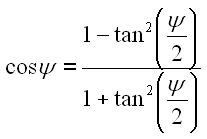 |
27 | |
 |
28 |
Jetzt substituieren wir den Tangens durch Gl. 29.
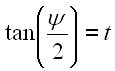 |
29 |
Gl. 29 setzen wir in Gl. 27 und Gl. 28 ein.
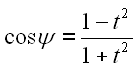 |
30 | |
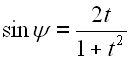 |
31 |
Nun können wir Gl. 30 und Gl. 31 in Gl. 25 einsetzen.
 |
32 |
Wenn wir Gl. 32 ausmultiplizieren und die Koeffizienten ein bischen sortieren erhalten wir eine quadratische Gleichung (siehe Anhang A4).
| 33 |
Die gleiche Umstellung machen wir mit Gl. 26. Wir ersetzen den Sinus und den Cosinus durch Gleichung B3 und B4.
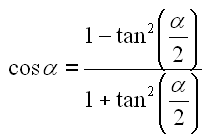 |
34 | |
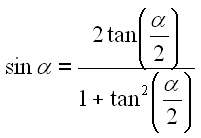 |
35 |
Jetzt substituieren wir den Tangens durch Gl. 36.
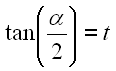 |
36 |
Gl. 36 setzen wir in Gl. 34 und Gl. 35 ein.
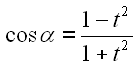 |
37 | |
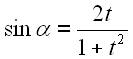 |
38 |
Nun setzen wir in Gl. 37 und Gl. 38 in Gl. 26 ein.
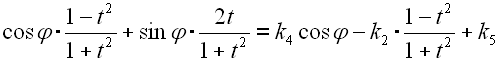 |
39 |
Wenn wir Gl. 39 ausmultiplizieren und die Koeffizienten ein bischen sortieren erhalten wir eine quadratische Gleichung (analog zu Anhang A4).
| 40 |
Aus den beiden quadratischen Gleichungen (Gl. 33 und Gl. 40) können wir jetzt die gesuchten Winkel berechnen. Fangen wir mit dem Schwingendrehwinkel psi an. Nach B5 lösen wir die quadratischen Gleichung Gl. 33.
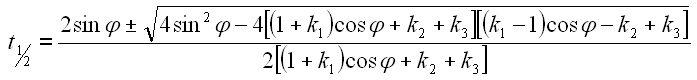 |
41 |
Gl. 41 kann durch Ausmultiplizieren noch vereinfacht werden (siehe Anhang A5).
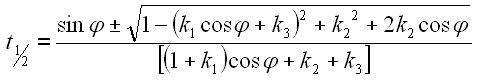 |
42 |
Mit Hilfe von Gl. 29 und Gl. 42 erhalten wir den gewünschten Ausdruck für den Winkel psi.
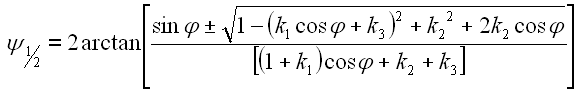 |
43 |
Analog dazu lösen wir die quadratische Gleichung Gl 40 und erhalten für den Winkel alpha.
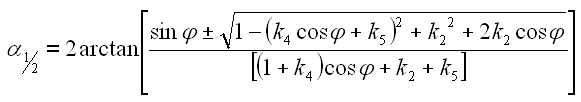 |
44 |
Um beide Gleichungen zu überprüfen setzten wir die Zahlen unseres Beispiels ein (siehe Anhang A6).
Zur Animation dieses Beispiels siehe Doppelschwinge.
Ein ähnlicher Lösungsansatz ist in folgendem Buch beschrieben.
| R. Hartenberg, J. Denavit |
| Kinematic Synthesis Of Linkages |
| McGraw-Hill Book Company |
| ISBN: |
| Online |
| [zurück] | [Inhaltsverzeichnis] | [vor] |