Anhang A
Für die Berechnung nehmen wir folgende Zahlenwerte.
| a = 7 | ||
| b = 5 | ||
| c = 4 | ||
| d = 3 | ||
| phi = 115° | ||
| alpha = 153,38° | ||
| psi = 64,45° |
Aus den Winkeln berechnen wir die Sinus und Cosinuswerte.
| sin(phi) = 0,9063 | ||
| cos(phi) = -0,4226 | ||
| sin(alpha) = 0,4481 | ||
| cos(alpha) = -0,8940 | ||
| sin(psi) = 0,9022 | ||
| cos(psi) = 0,4313 |
A1
![]()
-7 + 5 * 0,4313 - 4 * (-0,8940) = 3 * (-0,4226)
-7 + 2,1565 + 3,5760 = - 1,2678
- 1,2675 = - 1,2678
![]()
5 * 0,9022 - 4 * 0,4481 = 3 * 0,9063
2,7186 = 2,7189
Bis auf ein paar Rundungsfehler ist das Ergebnis korrekt.
A2
Quadrieren wir zuerst Gl. 12.
![]()
![]()
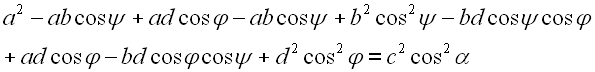
![]()
Quadrieren von Gl. 13.
![]()
![]()
![]()
Beide Gleichungen werden addiert.
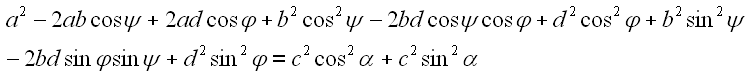
Durch Ausklammern läßt sich die Gleichung vereinfachen.
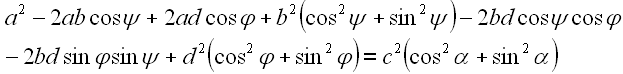
Mit Hilfe von Gleichung B1 erhält man.
![]()
Mit Hilfe von Gleichung B2 erhält man.
![]()
![]()
So erhalten wir Gl. 14.

A3
Quadrieren wir zuerst Gl. 15.
![]()
![]()
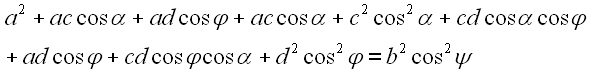
![]()
Quadrieren von Gl. 16.
![]()
![]()
![]()
Beide Gleichungen werden addiert.
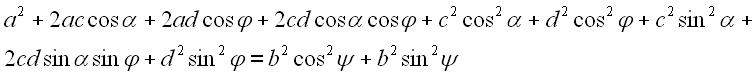
Durch Ausklammern läßt sich die Gleichung vereinfachen.
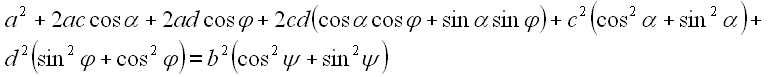
Mit Hilfe von Gleichung B1 erhält man.
![]()
Mit Hilfe von Gleichung B2 erhält man.
![]()
![]()
So erhalten wir Gl. 17.

A4

Beide Seiten werden mit (1+t2) multipliziert.
![]()
Ausmultiplizieren der Klammern.
![]()
Sortieren der Koeffizienten.
![]()
![]()
![]()
A5
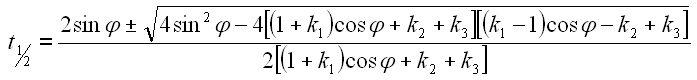
Die 4 unter der Wurzel kann gekürzt werden.
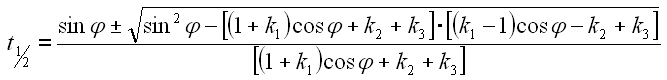
Jetzt betrachten wir nur den Wurzelausdruck und multiplizieren die Klammern aus.
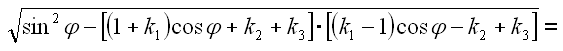
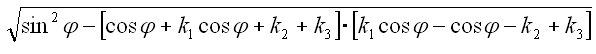
Multiplizieren wir nur die Klammern unter der Wurzel aus.
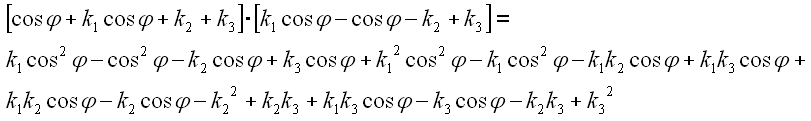
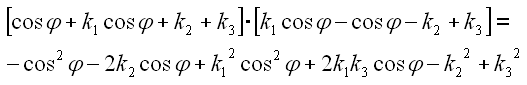
Diesen Ausdruck setzen wir wieder in die Wurzel ein.
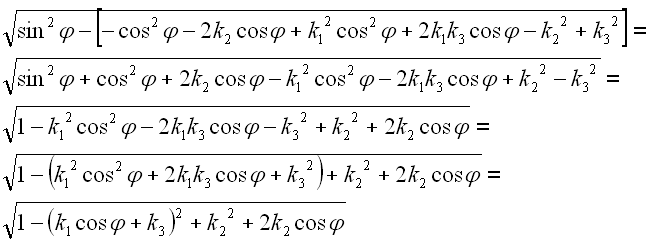
Damit erhalten wir die komplette Gleichung.
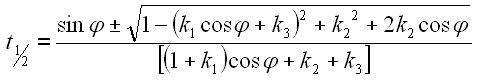
A6
Berechnen wir zuerst die Konstanten k1 bis k5.
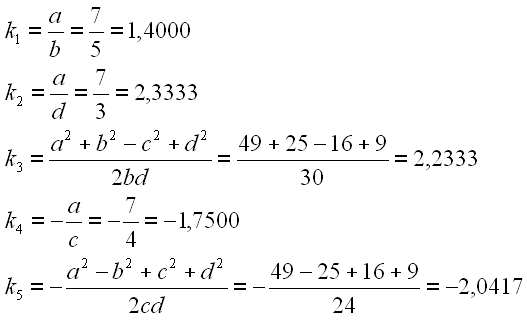
Die Winkel.
| sin(phi) = 0,9063 | ||
| cos(phi) = -0,4226 |
Jetzt setzen wir die Zahlen in Gl. 43 ein.
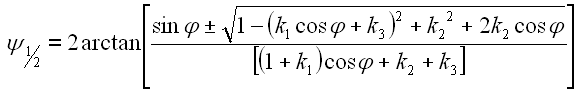

Jetzt setzen wir die Zahlen in Gl. 44 ein.
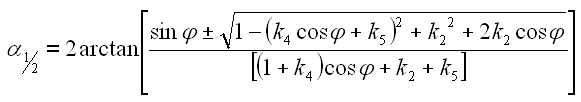

Beide Gleichungen liefern ein korrektes Ergebnis.