| [zurück] | Tschebyschow Geradführung |
[vor] |
Die Tschebyschow Geradführung wurde vom russischen Mathematiker Pafnuti Lwowitsch Tschebyschow (1821 - 1894) erfunden. Gelegentlich findet man auch die Schreibweise Tschebyschev oder Chebyshev.
Die Animation erfolgt wie bei der Doppelschwinge.
Die Stäbe b und d sind gleich lang. Die Länge der Stäbe leiten wir von der Konstanten R ab.
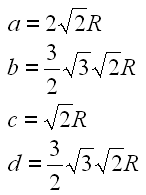 |
Mit R = 2,828 erhalten wir konkrete Werte für die 4 Stäbe.
| a = 8 | ||
| b = 10,39 | ||
| c = 4 | ||
| d = 10,39 |
Jetzt positionieren wir das Gelenkviereck so das Gestell a und Koppel c parallel sind.

Um die dafür nötigen Winkel phi und psi zu berechnen benutzen wir die zusätzlichen Linien e. Dadurch entstehen mit ACD und ABD 2 Dreiecke. e läßt sich dann aus dem Kosinussatz (siehe Anhang B6) berechnen. Da Kurbel und Schwinge gleich lang sind (d=b) lassen sich die Gleichungen vereinfachen.
 |
Nach dem Gleichsetzen lösen wir die Gleichung nach cos psi auf.
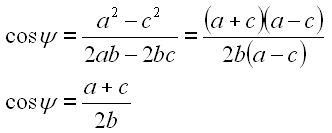 |
Wenn wir die Konstante R verwenden läßt sich die Gleichung weiter vereinfachen.
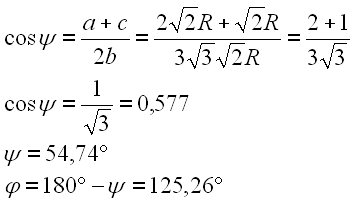 |
Da es sich um eine Doppelschwinge handelt müssen wir noch die Tot- bzw. Grenzlagen berechnen.
Berechnen wir zuerst phi1 von Totlage 1.

 |
Wenn wir die Konstante R verwenden läßt sich die Gleichung weiter vereinfachen.
 |
Berechnen wir phi2 von Totlage 2.

 |
Die Koppelkurve besteht aus zwei Teilen (rot und blau). Für jede Kurve ist Gl. 43 aus dem Gelenkviereck zuständig.
 |
||
 |
Für jeden Winkel phi der Kurbel existieren zwei Stellungen der Schwinge.
Kommen wir noch einmal zur Grundstellung zurück in dem Gestell a und Koppel c parallel sind. Kurbel d und Schwinge b schneiden sich im Punkt F und bilden zwei Dreiecke ABF und CDF. Die Umkreise dieser Dreiecke leiten sich wieder von der Konstanten R ab.

Download C4D Datei (Release 11) : Tschebyschow.zip
| [zurück] | [Inhaltsverzeichnis] | [vor] |