Kurbeltrieb mit Schränkung
|
[zurück] | Kurbeltrieb mit Schränkung |
[vor] | |
Unter Schränkung versteht man einen Versatz der Kurbelwelle bezogen auf die Kolbenachse. Eine Schränkung ist z.B. bei
VR Motoren nötig damit die Kolben ausreichend Platz haben.
Durch die Schränkung verändert sich die Lage der Totpunkte. Man unterscheidet Schränkung zur Druck- und zur Gegendruckseite.
Schränkung zur Druckseite.
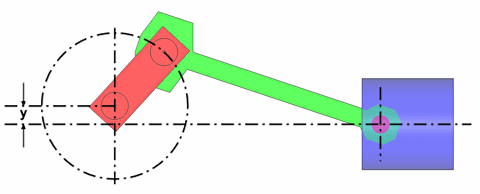
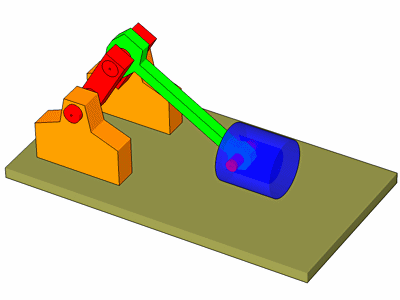
Schränkung zur Gegendruckseite.
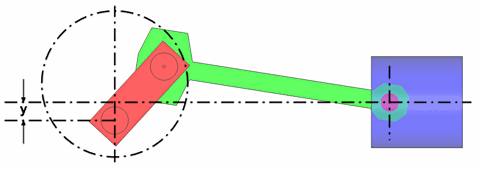
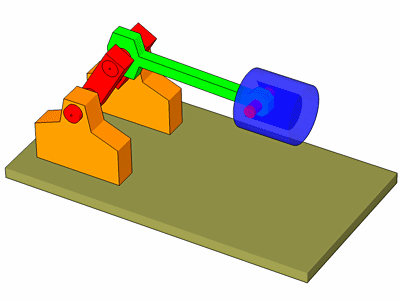
Für die Schränkung führen wir zwei weitere Konstanten ein.
| y | Schränkung bzw. Exzentrizität |
| e | Schränkungsverhältnis |
Das Schränkungsverhältnis wird wie folgt definiert.
 |
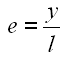19 |
Die beiden Totpunkte werden in der "Streck-" bzw. "Decklage" erreicht. Dabei zeigen Kurbelwelle und Pleuel geometrisch in die gleiche Richtung.
Im oberen Totpunkt (OT) bilden Schränkung, Kurbelradius und Pleuellänge ein rechtwinkliges Dreieck. Nach dem Satz von Pythagoras läßt sich die Kolbenposition sOT berechnen.
 |
20 |
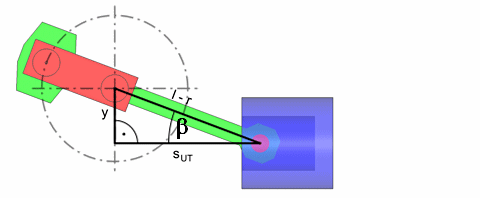
Im unteren Totpunkt (UT) bilden Schränkung, Kurbelradius und Pleuellänge ein rechtwinkliges Dreieck. Nach dem Satz von Pythagoras läßt sich die Kolbenposition sUT berechnen.
 |
21 |
Aus Gl. 20 ung Gl. 21 läßt sich der Kolbenhub berechnen.
 |
22 | |
 |
23 |
Um die Position des Kolbens sx zu berechnen benutzen wir eine Skizze in der der Kolben zwischen UT und OT positioniert wird.
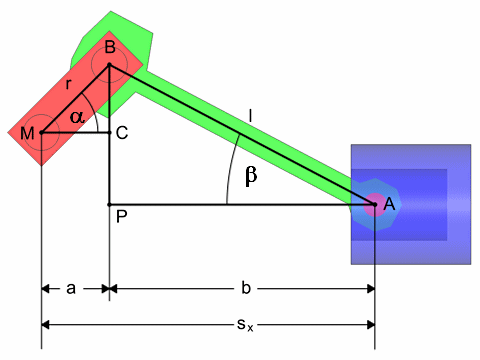
Für die Berechnung benutzen wir zwei rechtwinklige Dreiecke die aus den Punkten BCM und ABP gebildet werden. Die Position des Kolbens Kolbens sx setzt sich aus den beiden Teilstrecken a und b zusammen.
 |
4 |
Betrachten wir zunächst das Dreieck BCM. Die drei Seiten sind wie folgt definiert.
 |
24 | |
 |
25 | |
 |
26 |
Das Dreieck ABP. Die drei Seiten sind wie folgt definiert.
 |
27 | |
 |
28 | |
 |
29 | |
 |
30 |
Da der Winkel 
nicht bekannt ist müssen wir ihn aus Gl. 28 eliminieren.
Dazu nehmen wir zuerst den Sinus.
 |
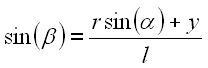31 |
Mit Hilfe von Gl. 2 (siehe Einfacher Kurbeltrieb) und Gl. 19 vereinfachen wir Gl. 31.
 |
32 |
Jetzt wandeln wir mit Hilfe von Gl. 13 (siehe Einfacher Kurbeltrieb) den Sinus in den Cosinus um.
 |
33 |
Gl. 33 setzen wir in Gl. 28 ein.
 |
34 |
Jetzt brauchen wir nur noch Gl. 34 und Gl. 25 in Gl. 4 einsetzen und erhalten die gewünschte Formel zur Berechnung der Kolbenposition sx.
 |
35 |
Zur Verwendung im Formel Node von Xpresso muß die Formel etwas umgeschrieben werden.
| xKolben=r*COS(w)+l*SQRT(1-SQR((r/l)*SIN(w)+(y/l))) | 36 |
Die Umsetzung in Cinema erfolgt im Prinzip wie beim einfachen Kurbeltrieb, nur der Kolben wird anders positioniert. Die Objekt-Achse des Kolbens und die Objekt-Achse der Kurbelwelle liegen in einer Ebene.
Download C4D Datei (Release 11) : Kurbel2.zipWeiterführende Links
| Motorlexikon | |
|
[zurück] | [Inhaltsverzeichnis] | [vor] | |