| [zurück] | Roberts Geradführung |
[vor] |
Bei der Roberts Geradführung wird die Drehbewegung der Kurbel in eine angenäherte Gerade umgewandelt.
Die geradlinige Bewegung findet allerdings nur in einem kleinen Teil der Bewegung statt.
Um das nachzubauen erstellen wir im ersten Schritt ein symmetrisches Gelenkviereck.
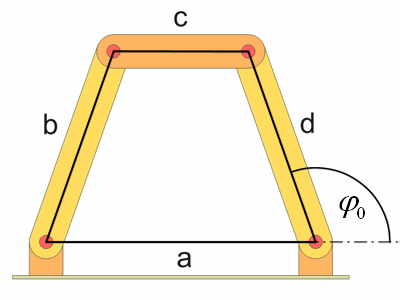
Die Stäbe haben folgende Längen, b und d sind gleich lang.
| a = 8 | ||
| b = 6 | ||
| c = 4 | ||
| d = 6 |
In dieser Stellung sind die Stäbe a und c parallel, der Winkel beträgt phi0. Der Winkel läßt sich leicht aus dem rechtwinkligen Teildreieck berechnen.
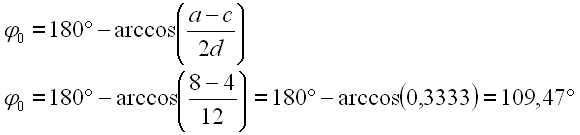 |
Dieses Gelenkviereck ist nicht umlauffähig, d.h. es existieren 2 Totpunkte. Die dazugehörenden Winkel phi1 und phi2 lassen sich leicht aus den entsprechenden Dreiecken berechnen.

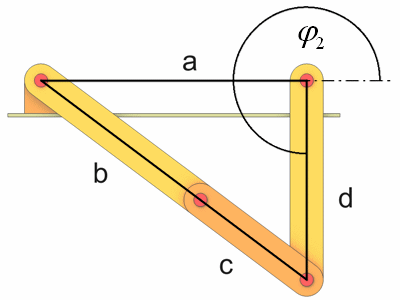
Es handelt sich in beiden Fällen um ein rechtwinkliges Dreieck wie man mit dem Satz des Pythagoras leicht überprüfen kann.
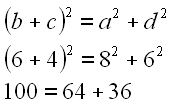 |
Die Winkel betragen.
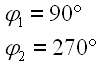 |
Das es sich bei diesem Beispiel um rechtwinklige Dreiecke handelt ergibt sich zufällig aus der Wahl der Längen a bis d.
Um daraus eine Geradführung zu machen benutzen wir eine sogenannte Koppelkurve. Dazu versehen wir die Koppel c mit einem Ausleger und machen aus dem Stab ein Dreieck. Der untere Punkt des Dreiecks zeichnet die Koppelkurve.
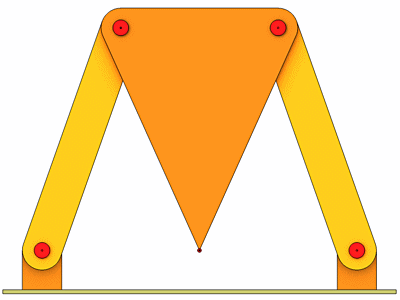
Die komplette Bewegung.
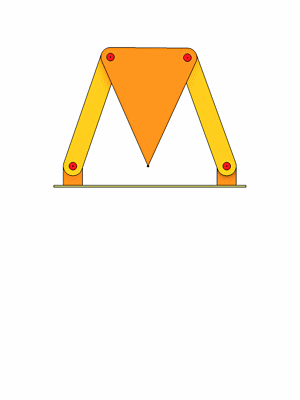
In dieser Darstellung ist die Koppelkurve eingezeichnet, ebenso die Bewegung der Kurbel und der Schwinge.
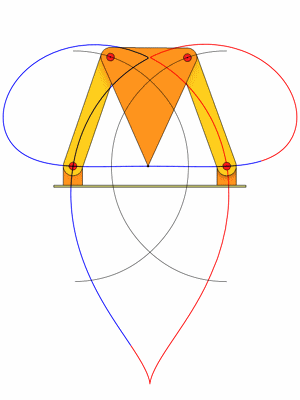
Die Koppelkurve besteht aus zwei Teilen (rot und blau). Für jede Kurve ist Gl. 43 aus dem Gelenkviereck zuständig.
 |
||
 |
Für jeden Winkel phi der Kurbel existieren zwei Stellungen der Schwinge.
Download C4D Datei (Release 11) : Roberts.zip
| [zurück] | [Inhaltsverzeichnis] | [vor] |