| [zurück] | Evans Geradführung |
[vor] |
Die Evans Geradführung wurde vom amerikanischen Ingenieur Oliver Evans (1755 - 1819) erfunden.
Die Animation in Cinema erfolgt wie bei der Doppelschwinge. Die Animation zeigt nur den oberen linearen Bereich.
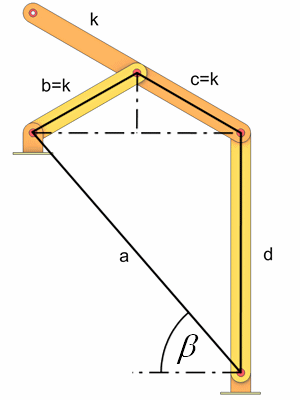
Die Stäbe b und c sind gleich lang und leiten sich von der Konstante k ab. Die Länge von Stab d kann frei gewählt werden, in diesem Beispiel ist d=2k. Die Stäbe haben folgende Längen.
| a =15,87 | ||
| b = 6 | ||
| c = 6 | ||
| d = 12 |
Die Länge des Stabes a wird aus den Längen der anderen Stäbe berechnet, dazu benutzen wir das rechtwinklige Dreieck.
Mit d=2k und b=k läßt sich die Gleichung vereinfachen.
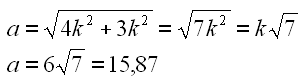 |
In dieser Darstellung befinden sich beide Lager nicht gemeinsam auf der x-Achse. Bei der Berechnung der Winkel wird das aber vorausgesetzt (siehe Gelenkviereck). Dieses Problem können wir umgehen wenn wir erst das fertige Modell in diese Position drehen (um den Winkel beta).
Der Winkel beta läßt sich leicht aus dem rechtwinkligen Dreieck berechnen.
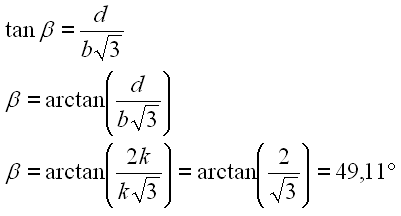 |
Da es sich um eine Doppelschwinge handelt müssen wir noch die Tot- bzw. Grenzlagen berechnen.
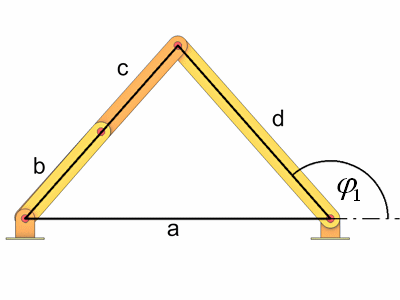
Berechnen wir zuerst phi1 von Totlage 1.
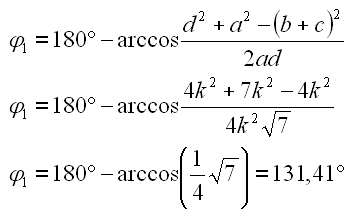 |
Berechnen wir phi2 von Totlage 2.
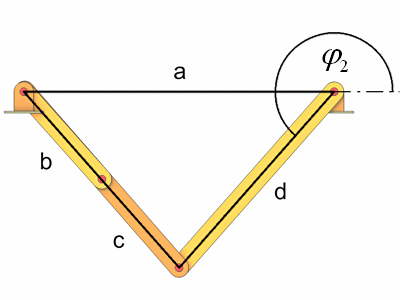
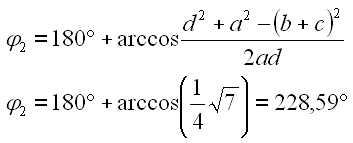 |
Die Koppelkurve besteht aus zwei Teilen (rot und blau). Für jede Kurve ist Gl. 43 aus dem Gelenkviereck zuständig.
 |
||
 |
Die folgende Abbildung zeigt die komplette Koppelkurve und die Bewegung der Kurbel und der Schwinge.
Download C4D Datei (Release 11) : Evans.zip
| [zurück] | [Inhaltsverzeichnis] | [vor] |